课后习题

习题涵盖了自由电子费米气体模型的核心概念。这部分知识通常是理解金属导电性、半导体物理以及能带理论前奏的基础。

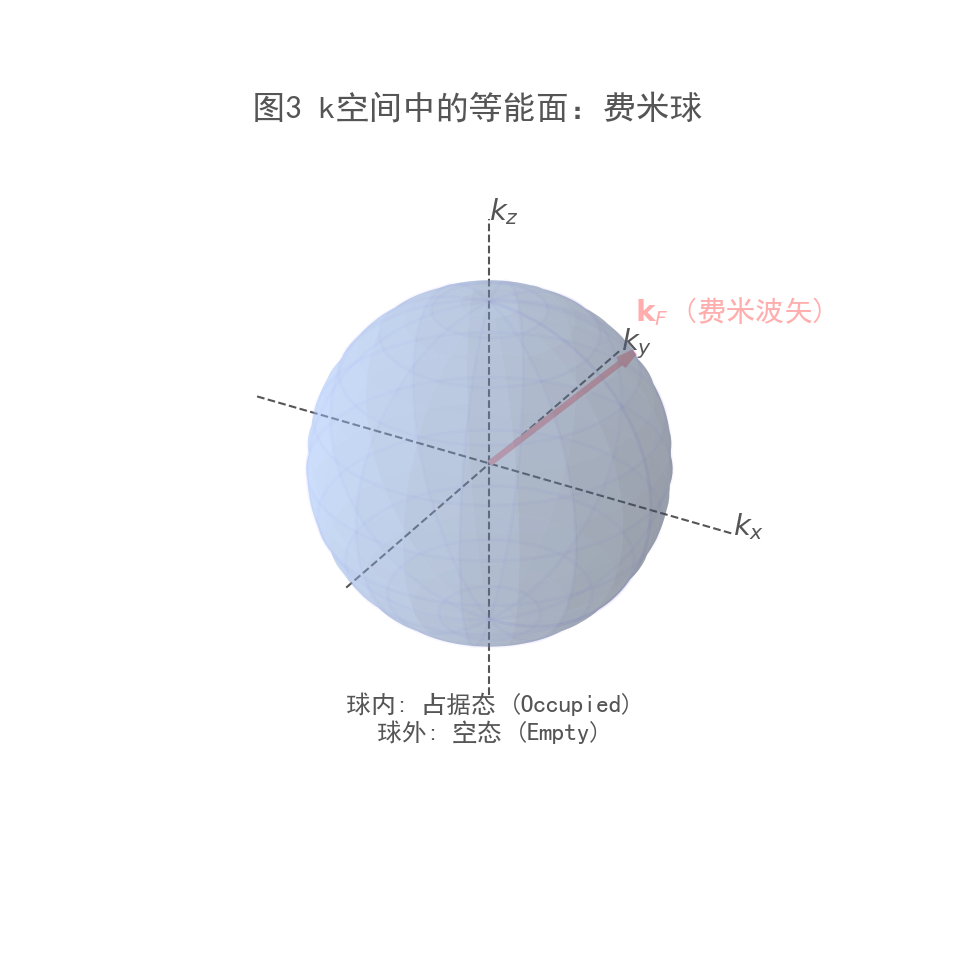
图3：k空间与费米球
对应 习题二 和 习题四。
展示三维 k 空间中，电子如何填充成一个球体。
直观展示 $k_x, k_y, k_z$ 坐标轴以及费米波矢 $k_F$（半径）。

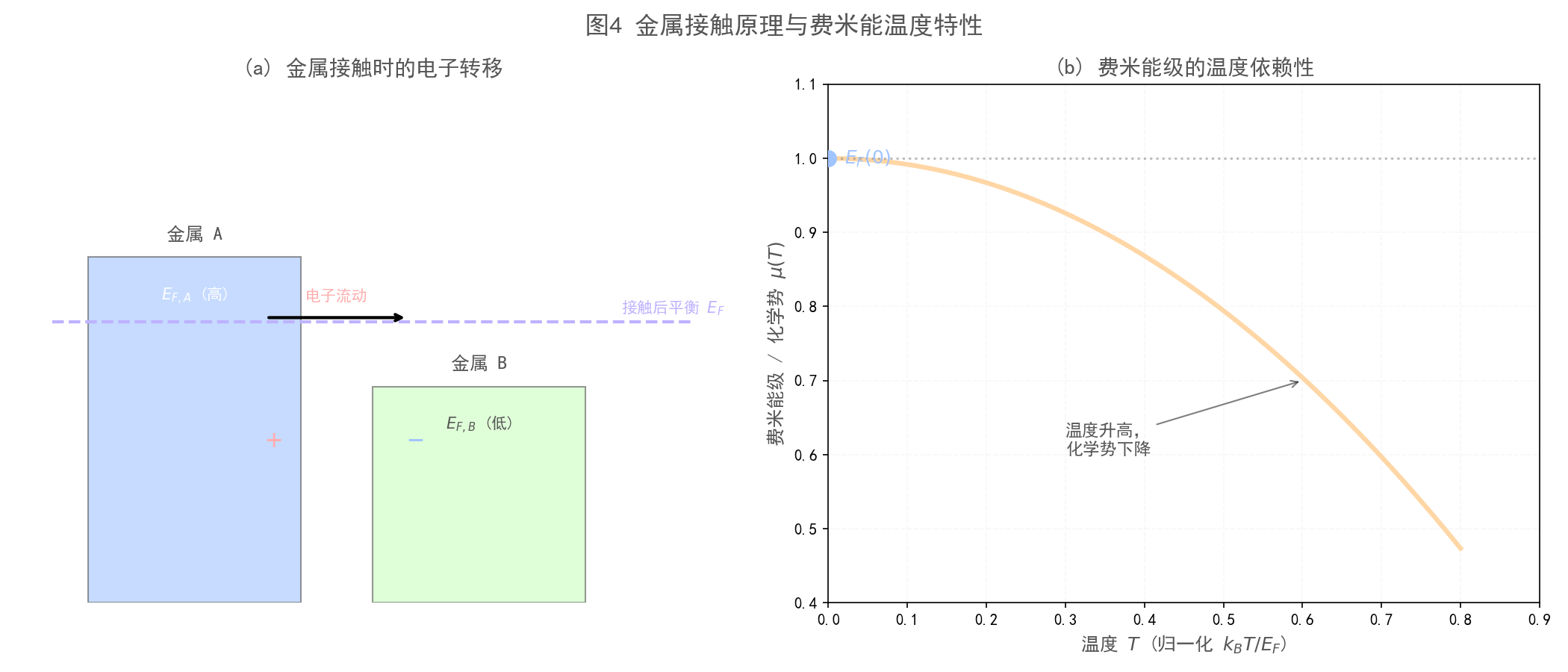
图4：接触电势差与费米能温度特性**
对应 习题三 和 习题七。
左图：展示两种费米能级不同的金属接触前后的能级变化，解释电子流向。
右图：展示化学势 $\mu$ 随温度 $T$ 的变化曲线（索末菲展开），直观显示为何 $T>0$ 时费米能略低。

习题一：银的费米参数计算

【问题】
若把银看成具有球形费米面的单价金属，计算费米能、费米温度、费米球半径、费米速度、横截面积及平均自由程。
（参数：密度 $10.5\text{g/cm}^3$，原子量 $107.87$，电阻率 $\rho_{295\text{K}} = 1.61 \times 10^{-6} \Omega \cdot \text{cm}$，$\rho_{20\text{K}} = 0.038 \times 10^{-6} \Omega \cdot \text{cm}$）

【知识点】

• 自由电子模型：假设电子在晶体中像气体一样自由运动，忽略离子势场起伏。
• 电子浓度 $n$：单位体积内的电子数。
• 费米波矢 $k_F$：费米球半径，与电子浓度相关。
• 费米能 $E_F$：绝对零度下电子占据的最高能级。
• 德鲁德（Drude）电导率公式：联系微观弛豫时间 $\tau$ 与宏观电阻率 $\rho$。

【思路】

1. 计算电子浓度 $n$。
2. 利用 $n$ 求费米波矢 $k_F$（费米球半径）。
3. 利用 $k_F$ 求费米能 $E_F$、费米温度 $T_F$ 和费米速度 $v_F$。
4. 利用电阻率求弛豫时间 $\tau$，进而求平均自由程 $l = v_F \tau$。

【解答】

1. 计算电子浓度 $n$

银是单价金属，每个原子提供 1 个自由电子。利用密度 $\rho_m$ 和摩尔质量 $M$ 计算：

$$ n = \frac{Z \rho_m N_A}{M} $$

代入数据（注意统一单位为 SI 制，即 $\text{m}^{-3}$）：
$\rho_m = 10.5 \times 10^3 \text{kg/m}^3$，$M = 107.87 \times 10^{-3} \text{kg/mol}$，$N_A = 6.02 \times 10^{23} \text{mol}^{-1}$。

$$ n = \frac{1 \times 10.5 \times 10^3 \times 6.02 \times 10^{23}}{107.87 \times 10^{-3}} $$

$$ n \approx 5.86 \times 10^{28} \text{m}^{-3} $$

2. 计算费米球半径（费米波矢）$k_F$

根据泡利不相容原理和态密度推导：

$$ k_F = (3\pi^2 n)^{1/3} $$

$$ k_F = (3 \times \pi^2 \times 5.86 \times 10^{28})^{1/3} $$

$$ k_F \approx 1.20 \times 10^{10} \text{m}^{-1} $$

3. 计算费米能 $E_F$

$$ E_F = \frac{\hbar^2 k_F^2}{2m} $$

$$ E_F = \frac{(1.055 \times 10^{-34})^2 \times (1.20 \times 10^{10})^2}{2 \times 9.11 \times 10^{-31}} \approx 8.82 \times 10^{-19} \text{J} $$

转换为电子伏特 ($1\text{eV} = 1.6 \times 10^{-19}\text{J}$)：

$$ E_F \approx 5.51 \text{eV} $$

4. 计算费米温度 $T_F$

$$ T_F = \frac{E_F}{k_B} $$

$$ T_F = \frac{8.82 \times 10^{-19}}{1.38 \times 10^{-23}} \approx 6.39 \times 10^4 \text{K} $$

5. 计算费米速度 $v_F$

$$ v_F = \frac{\hbar k_F}{m} $$

$$ v_F = \frac{1.055 \times 10^{-34} \times 1.20 \times 10^{10}}{9.11 \times 10^{-31}} \approx 1.39 \times 10^6 \text{m/s} $$

6. 计算费米球面的横截面积 $S_F$

$$ S_F = \pi k_F^2 $$

$$ S_F = \pi \times (1.20 \times 10^{10})^2 \approx 4.52 \times 10^{20} \text{m}^{-2} $$

7. 计算平均自由程 $l$

根据电导率公式 $\sigma = \frac{ne^2\tau}{m}$ 和电阻率 $\rho_r = 1/\sigma$：

$$ \rho_r = \frac{m}{ne^2\tau} \Rightarrow \tau = \frac{m}{ne^2\rho_r} $$

平均自由程 $l = v_F \tau$：

$$ l = v_F \frac{m}{ne^2\rho_r} $$

注意单位：$1.61 \times 10^{-6} \Omega \cdot \text{cm} = 1.61 \times 10^{-8} \Omega \cdot \text{m}$。

在 295 K 时：

$$ l_{295K} = \frac{1.39 \times 10^6 \times 9.11 \times 10^{-31}}{5.86 \times 10^{28} \times (1.6 \times 10^{-19})^2 \times 1.61 \times 10^{-8}} $$

$$ l_{295K} \approx 5.2 \times 10^{-8} \text{m} = 520 \text{\AA} $$

在 20 K 时：

$$ l_{20K} = l_{295K} \times \frac{\rho_{295K}}{\rho_{20K}} $$

$$ l_{20K} = 5.2 \times 10^{-8} \times \frac{1.61}{0.038} \approx 2.2 \times 10^{-6} \text{m} = 2.2 \mu\text{m} $$

习题二：k空间等能面形状

【问题】
依照量子的自由电子的理论， k 空间中电子的等能面是？

【知识点】

• 自由电子能量公式：$E(k) = \frac{\hbar^2 k^2}{2m} = \frac{\hbar^2 (k_x^2 + k_y^2 + k_z^2)}{2m}$。

【思路】
观察能量 $E$ 与波矢 $\boldsymbol{k}$ 的关系。

【解答】
球面。
因为能量 $E$ 仅与波矢的大小 $|\boldsymbol{k}|$ 有关（各向同性），所以等能面方程 $k_x^2 + k_y^2 + k_z^2 = \text{const}$ 描述了一个球面。

习题三：接触电势差

【问题】
两种不同金属接触后，费米能级高的带（ ）电，费米能级低的带（ ）电。

【知识点】

• 化学势平衡：电子总是从高化学势（高费米能级）流向低化学势（低费米能级），直到系统平衡，费米能级拉平。
• 接触电势：电子流出使物体带正电，流入使物体带负电。

【思路】
分析电子流向：高 $E_F \rightarrow$ 低 $E_F$。

【解答】
正；负。
电子从费米能级高的金属流向费米能级低的金属。失去电子的金属带正电，获得电子的金属带负电。

习题四：费米面的定义

【问题】
什么是费米面？

【知识点】

• k空间分布：绝对零度下，电子在k空间中的填充情况。

【思路】
结合泡利不相容原理和能量最低原理描述k空间的填充边界。

【解答】
在绝对零度 ($T=0\text{K}$) 时，k空间中电子填充态与未填充态的分界面称为费米面。对于自由电子气体，费米面是一个半径为 $k_F$ 的球面。费米面内的状态全被占据，费米面外的状态全空。

习题五：费米-狄拉克分布

【问题】
在 $T \ne 0 \text{K}$ 时，$E_F$ 上电子占有几率为（ ）。

【知识点】

• 费米分布函数：$f(E) = \frac{1}{e^{(E-E_F)/k_B T} + 1}$。

【思路】
将 $E = E_F$ 代入公式。

【解答】
0.5 (或 1/2)。
计算：$f(E_F) = \frac{1}{e^0 + 1} = \frac{1}{1+1} = \frac{1}{2}$。这具有重要的物理意义：费米能级是电子出现概率为50%的能量位置。

习题六：费米能级名词解释

【问题】
名词解释：费米能级。

【知识点】

• 物理定义：等同于热力学中的化学势 $\mu$。
• 直观定义：$T=0\text{K}$ 时的最高填充能级。

【解答】
费米能级 ($E_F$) 是描述费米子系统（如电子）统计性质的重要参数。

1. 在绝对零度 ($T=0\text{K}$) 时：它是电子所填充的最高能级的能量值。
2. 在任意温度 ($T>0\text{K}$) 时：它是电子占据概率为 1/2 的能级位置，在热力学上等同于电子系统的化学势 $\mu$。

习题七：费米能的温度依赖性

【问题】
同一晶体在 $T = 0 \text{K}$ 时的费米能（ ）$T \ne 0 \text{K}$ 时的费米能。

【知识点】

• 索末菲展开（Sommerfeld expansion）：描述化学势（即费米能级）随温度的变化关系。

【思路】
$$E_F(T) \approx E_F(0) \left[ 1 - \frac{\pi^2}{12} \left( \frac{k_B T}{E_F(0)} \right)^2 \right]$$

【解答】
大于（或 略大于）。
根据索末菲展开式，随着温度 $T$ 升高，化学势 $\mu$（即 $T \neq 0$ 时的费米能级）会略微下降。
即 $E_F(0) > E_F(T)$。
(注：在许多粗略的工程近似中，常认为 $E_F$ 基本不变，但若考察物理原理，它是随着温度变大而减小的)