费米能级与自由电子费米气体
费米能级(Fermi Level)是凝聚态物理学中一个极其重要的概念,特别是在描述金属、半导体和绝缘体的电子行为时。它源于量子力学中的泡利不相容原理以及统计力学中的费米-狄拉克统计。理解费米能级对于掌握材料的电学、热学和磁学性质至关重要。
本章将主要基于自由电子模型来阐述费米能级的基本理论,并扩展到其在不同温度下的行为以及在材料接触时的应用。
1. 自由电子模型与泡利不相容原理
自由电子模型是研究金属性质最简单的量子力学模型。它假设:
- 金属中的价电子脱离原子核束缚,成为“自由电子”,在整个晶体中运动。
- 这些自由电子之间没有相互作用(独立电子近似)。
- 自由电子与周期性排列的离子实之间也没有相互作用,或者说,周期性势场被平均化为一个常数,电子的势能为零。
在这样的模型下,电子的能量 $E$ 仅由其动能决定。在三维空间中,一个动量为 $\boldsymbol{p}$ 的自由电子的能量为:
$$ E = \frac{p^2}{2m} = \frac{\hbar^2 k^2}{2m} $$
其中 $m$ 是电子质量,$\hbar$ 是约化普朗克常数,$\boldsymbol{k} = \boldsymbol{p}/\hbar$ 是电子的波矢。
泡利不相容原理规定:在任何一个量子态中,最多只能容纳两个自旋方向相反的电子。这意味着在能量最低原则下,电子将从最低能量态开始填充,每个能量态(考虑自旋)填充两个电子,直到所有电子都被容纳。
2. 电子浓度与k空间填充
电子浓度 ($n$) 是单位体积内的自由电子数目,是计算费米能级的基础。对于单价金属(如银),每个原子贡献一个自由电子。电子浓度可以通过以下公式从材料的宏观参数中计算得到:
$$ n = \frac{Z \rho_m N_A}{M} $$
其中:
- $Z$ 为每个原子贡献的自由电子数(对于单价金属 $Z=1$)。
- $\rho_m$ 为材料的质量密度。
- $N_A$ 为阿伏伽德罗常数。
- $M$ 为材料的摩尔质量(相对原子质量)。
根据量子力学,一个具有波矢 $\boldsymbol{k}$ 的电子对应一个微观量子态。在k空间中,每个电子态占据的体积为 $(2\pi/L)^3$,其中 $L$ 是晶体的边长。为了将每个自旋方向的电子态都计算在内,我们需要乘以一个自旋简并因子 $2$。
3. 费米波矢 ($k_F$) 和费米球
在绝对零度 ($T=0\text{K}$) 时,根据泡利不相容原理和能量最低原则,电子将占据k空间中能量最低的所有量子态,直到所有的 $N$ 个自由电子都被容纳。这些被占据的态在k空间中形成一个球体,这个球体被称为费米球。费米球的半径即为费米波矢 ($k_F$)。
费米球内部的所有态都被占据,球外部的所有态都是空的。费米波矢 $k_F$ 与电子浓度 $n$ 之间的关系可以推导如下:
在一个体积为 $V = L^3$ 的晶体中,k空间的总态密度为 $\frac{V}{(2\pi)^3}$。考虑到电子的自旋简并(每个k态可容纳2个电子),费米球内可容纳的总电子数为:
$$ N = 2 \times \frac{V_k}{(2\pi)^3} = 2 \times \frac{\frac{4}{3}\pi k_F^3}{(2\pi)^3} = \frac{V k_F^3}{3\pi^2} $$
单位体积的电子数(即电子浓度)为 $n = N/V$:
$$ n = \frac{k_F^3}{3\pi^2} $$
因此,费米波矢 $k_F$ 可以表示为:
$$ k_F = (3\pi^2 n)^{1/3} $$
4. 费米能 ($E_F$)
费米能 ($E_F$) 是在绝对零度 ($T=0\text{K}$) 时,系统中电子所能占据的最高能量。它对应于费米球面上电子的能量。
将费米波矢 $k_F$ 代入自由电子的能量公式 $E = \frac{\hbar^2 k^2}{2m}$,即可得到费米能的表达式:
$$ E_F = \frac{\hbar^2 k_F^2}{2m} = \frac{\hbar^2}{2m} (3\pi^2 n)^{2/3} $$
费米能的典型值在几个电子伏特(eV)左右,这表明即使在绝对零度,电子系统仍具有相当高的能量。
5. 费米速度 ($v_F$) 和费米温度 ($T_F$)
费米速度 ($v_F$) 是在绝对零度时,费米面上电子的运动速度。它可以通过将费米波矢 $k_F$ 代入电子动量与速度的关系 $p = \hbar k = mv$ 得到:
$$ v_F = \frac{\hbar k_F}{m} = \frac{\hbar}{m} (3\pi^2 n)^{1/3} $$
费米速度通常非常高,接近光速的百分之一。
费米温度 ($T_F$) 是与费米能相对应的特征温度,定义为:
$$ T_F = \frac{E_F}{k_B} $$
其中 $k_B$ 是玻尔兹曼常数。费米温度的典型值在几万开尔文(K)到十几万开尔文,远高于室温。这表明在室温下,只有费米能级附近的少数电子的热运动能量才能与费米能相比较,大部分电子仍处于简并态。
6. 费米面 (Fermi Surface)
费米面是在k空间中,绝对零度下已填充态与未填充态之间的分界面。
- 对于自由电子模型:费米面是一个半径为 $k_F$ 的理想球面。费米球内的所有量子态都被占据,费米球外的所有量子态都是空的。
- 对于真实晶体:由于周期性晶格势场的作用,能带结构 $E(\boldsymbol{k})$ 不再是简单的二次方关系,费米面往往是复杂的非球面形状。
费米面在描述金属的电学、磁学和热学性质中扮演着核心角色。只有费米面附近的电子才能在电场作用下被激发到更高的能量态,从而参与导电。
7. 费米-狄拉克分布函数 ($f(E)$) 与电子占有几率
在非零温度 ($T \ne 0\text{K}$) 下,电子的占有几率不再是简单的“全占满”或“全空”,而是由费米-狄拉克分布函数给出:
$$ f(E) = \frac{1}{e^{(E - \mu)/k_B T} + 1} $$
其中 $\mu$ 是化学势。在固体物理中,当温度 $T$ 不为零时,费米能级通常指的就是这个化学势 $\mu$。
在 $T=0\text{K}$ 时:
- 当 $E < E_F$ 时,$f(E) = 1$(所有态被完全占据)。
- 当 $E > E_F$ 时,$f(E) = 0$(所有态完全空)。
- 在绝对零度下,费米能级正好是填充态和空态的分界线。
在 $T \ne 0\text{K}$ 时:
- 当 $E = \mu$ (即费米能级)时:
$$f(\mu) = \frac{1}{e^0 + 1} = \frac{1}{2}$$
这意味着在非零温度下,费米能级是电子占据概率为 1/2 (50%) 的能级位置。 - 费米能级附近的电子(能量在 $\mu \pm k_B T$ 范围内)的占据几率会偏离0或1,形成一个过渡区。
- 当 $E = \mu$ (即费米能级)时:
图1:费米-狄拉克分布函数 ($f(E)$)
展示在绝对零度 ($T=0$) 和非零温度 ($T>0$) 下,电子占据概率随能量的变化。特别需要注意费米能级 $E_F$ 处概率为 0.5的特征。
8. 费米能级的温度依赖性
严格来说,费米能级(化学势)是随着温度变化的。对于金属,其费米能级的温度依赖性通常由索末菲展开式给出:
$$ \mu(T) = E_F(0) \left[ 1 - \frac{\pi^2}{12} \left( \frac{k_B T}{E_F(0)} \right)^2 \right] $$
其中 $E_F(0)$ 是在 $T=0\text{K}$ 时的费米能。
这个公式表明:
- 在 $T=0\text{K}$ 时,$\mu(0) = E_F(0)$。
- 在 $T \ne 0\text{K}$ 时,化学势 $\mu(T)$ 会略微小于 $E_F(0)$。这意味着 $T=0\text{K}$ 时的费米能略大于 $T \ne 0\text{K}$ 时的费米能。
- 由于费米温度 $T_F$ 通常远高于室温 ($E_F(0) \gg k_B T$),所以费米能级随温度的变化非常微小,在许多实际应用中常被近似为常数。
图2:自由电子态密度与电子填充 ($g(E)$ & Occupancy)
展示三维自由电子气体的态密度抛物线形状 ($g(E) \propto \sqrt{E}$)。在 $T=0$ 时锐利的填充边界,以及 $T>0$ 时费米面附近的“热激发”模糊边界。
9. 费米能级在金属接触中的应用
费米能级(化学势)是决定电子在不同材料之间如何移动的关键。当两种不同的金属接触时,电子将从化学势高(费米能级高)的区域流向化学势低(费米能级低)的区域,直到整个系统的化学势(费米能级)达到平衡,即在整个接触区域内费米能级拉平。
这种电子的重新分布会导致:
- 费米能级高的金属失去电子,从而带正电。
- 费米能级低的金属获得电子,从而带负电。
这种电荷分离会在接触界面产生一个接触电势差,其大小取决于两种金属初始费米能级的高度差。
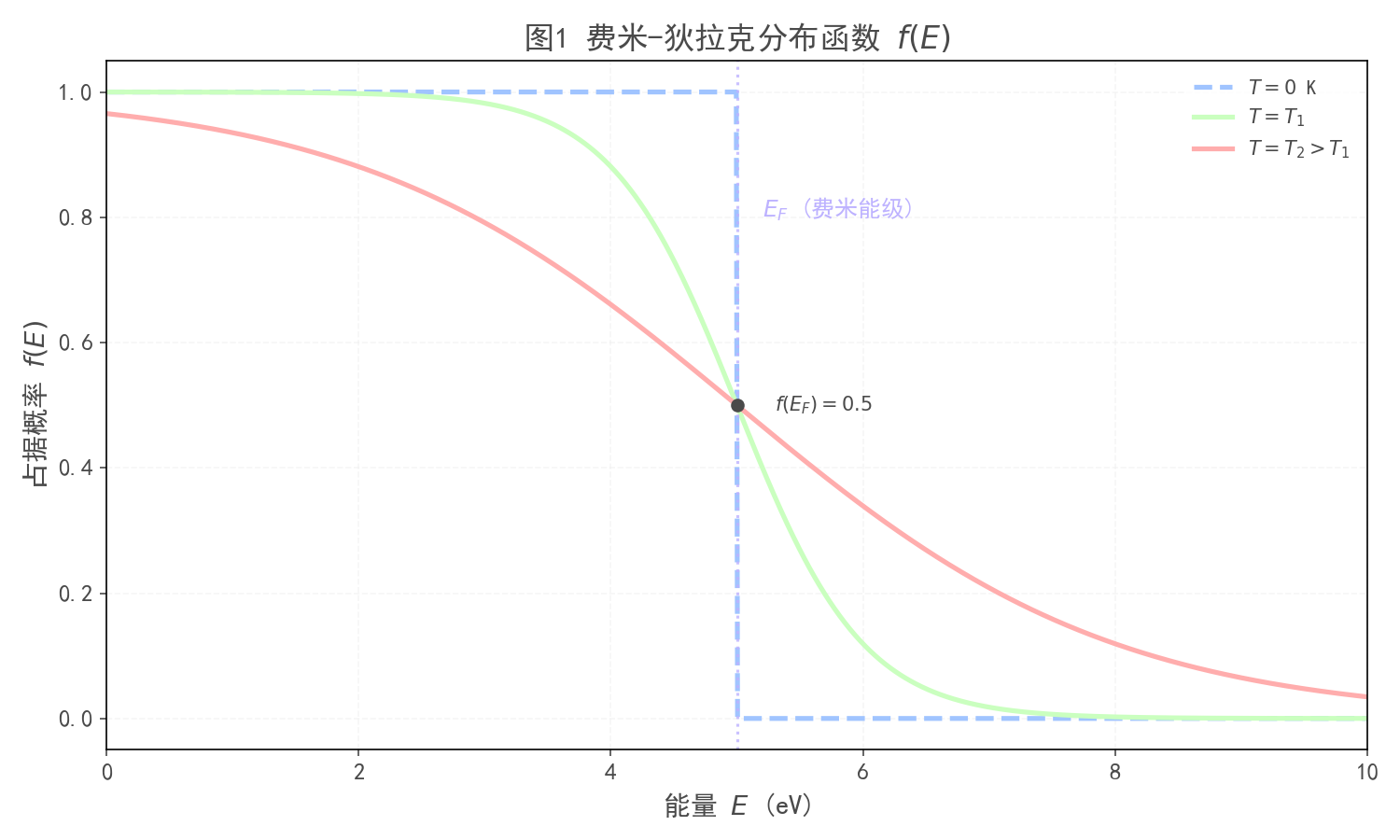
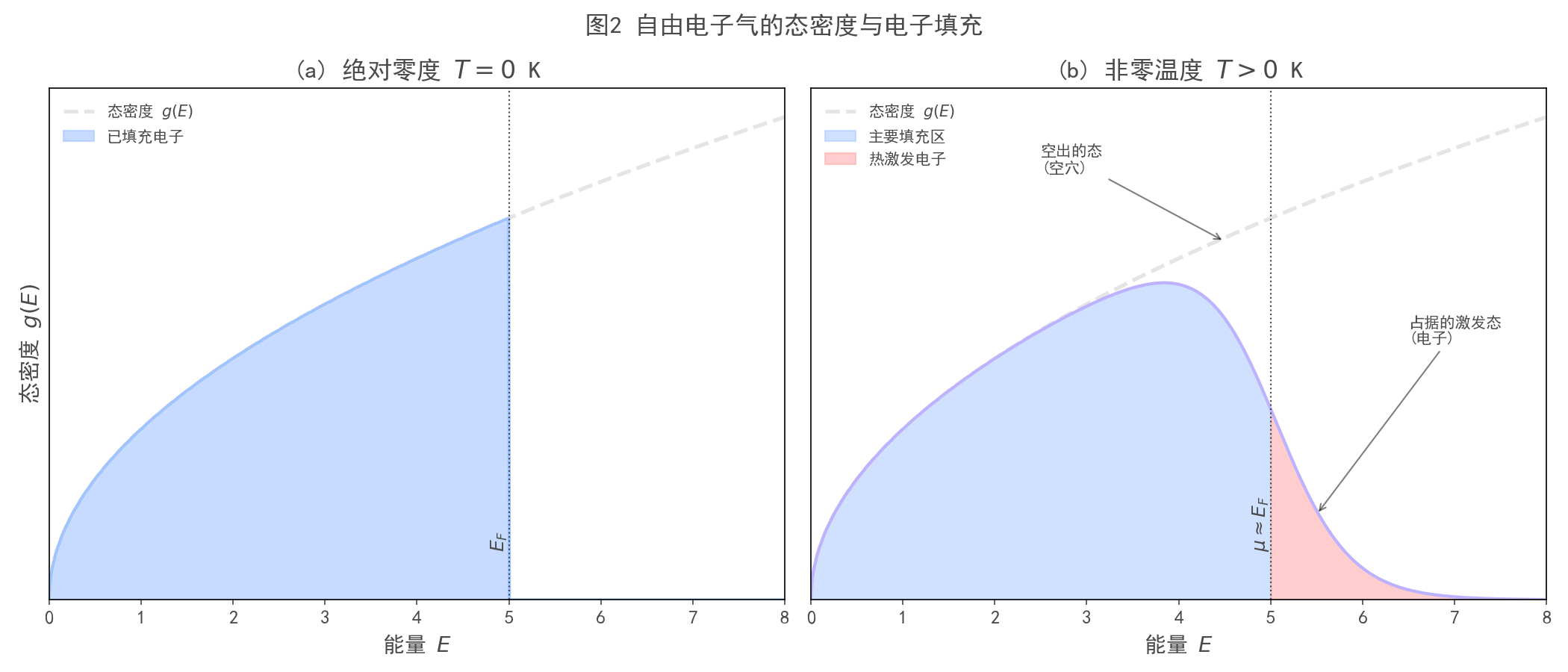 图2:自由电子态密度与电子填充 ($g(E)$ & Occupancy)
图2:自由电子态密度与电子填充 ($g(E)$ & Occupancy)
便签纸
这里还没有关于这篇笔记的便签