理论推导

本章从量子力学的微观视角出发，利用波包叠加原理构建了电子在晶体中的运动图景，确立了群速度 $\boldsymbol{v} = \frac{1}{\hbar}\nabla_{\boldsymbol{k}}E(\boldsymbol{k})$ 与能带梯度的核心联系；在此基础上，通过引入外力做功与能量全微分的等价性，推导出准动量定理 $\boldsymbol{F} = \hbar \frac{d\boldsymbol{k}}{dt}$，并进一步将加速度与外力的关系映射为倒有效质量张量 $(\frac{1}{m^*})_{\alpha\beta} = \frac{1}{\hbar^2}\frac{\partial^2 E}{\partial k_\alpha \partial k_\beta}$，从而赋予了能带曲率以动力学质量的物理意义；随后，理论严格证明了满带电子由于速度矢量 $\sum \boldsymbol{v}(\boldsymbol{k}) = 0$ 的对称抵消而不产生宏观电流，进而通过空缺状态的等效处理导出了空穴的输运方程 $\boldsymbol{J}_h = +e\boldsymbol{v}_e$，最终结合磁场下的洛伦兹力模型，推导出了回旋共振频率 $\omega_c = \frac{eB}{m^*}$，完美实现了从微观能带结构到宏观实验测量（有效质量测定）的逻辑闭环。

电子波包与群速度的构建

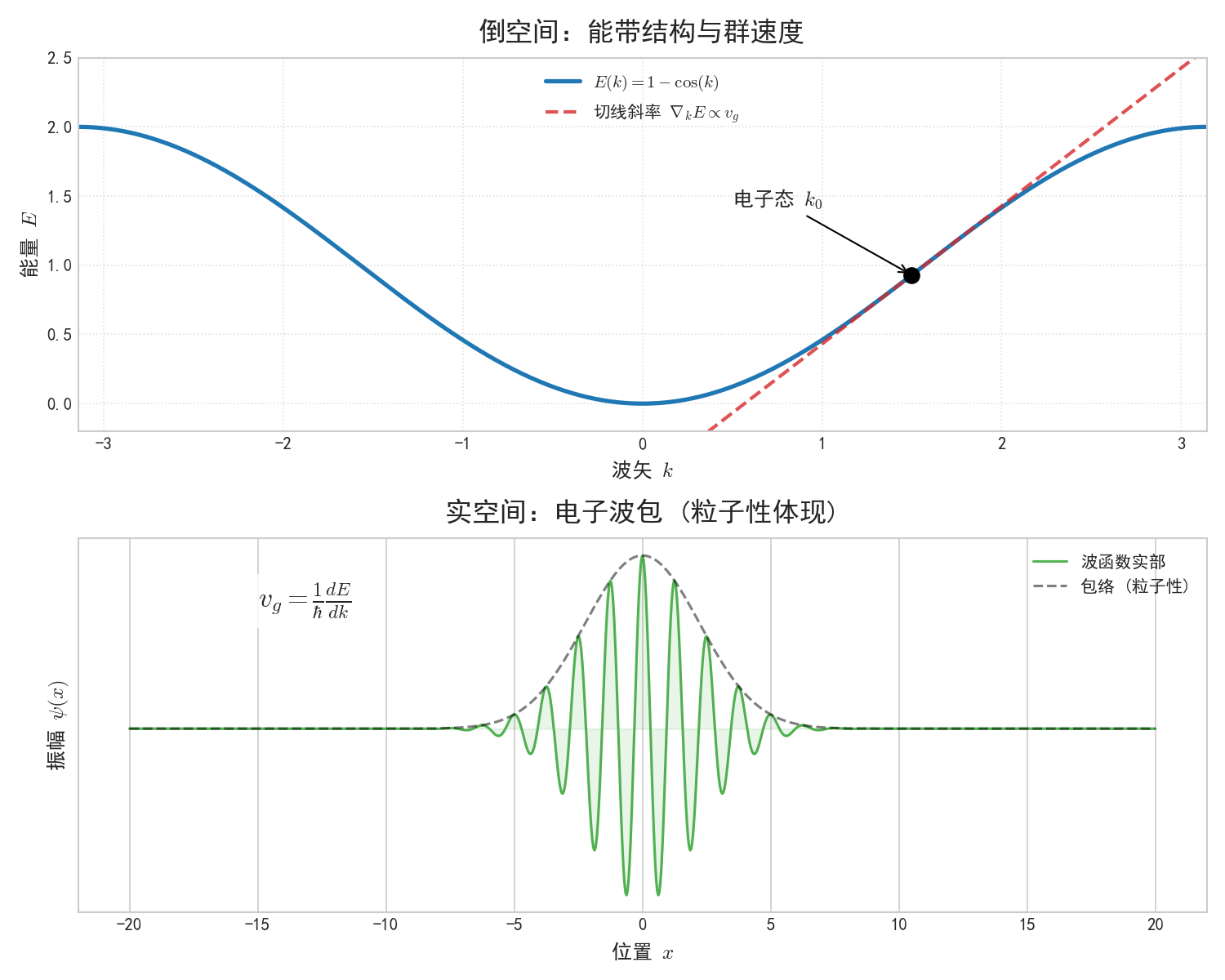
波包在实空间的形式，以及其速度（群速度）是如何由倒空间（k空间）中能带的斜率决定的。

在晶体中，单一的布洛赫波 $\psi_k$ 弥散在整个晶体中，无法确定位置。为了描述“电子粒子”的运动，我们需要构建一个由不同波矢 $\boldsymbol{k}$ 叠加而成的波包。

波包中心的运动速度即为群速度。根据量子力学原理，能量 $E$ 与角频率 $\omega$ 的关系为 $E = \hbar \omega$。

群速度 $\boldsymbol{v}$ 的定义为：

$$ \boldsymbol{v} = \nabla_{\boldsymbol{k}} \omega(\boldsymbol{k}) $$

将能量关系代入，得到晶体电子速度的核心公式：

$$ \boldsymbol{v}(\boldsymbol{k}) = \frac{1}{\hbar} \nabla_{\boldsymbol{k}} E(\boldsymbol{k}) $$

这一公式表明，电子的速度完全由能带结构 $E(\boldsymbol{k})$ 在 $\boldsymbol{k}$ 空间的梯度（斜率）决定。

外力作用下的准动量定理

当外力 $\boldsymbol{F}$ 作用于电子时，外力对电子做功，导致电子能量发生改变。

根据功能原理，在时间 $dt$ 内，外力做功等于能量的变化：

$$ dE = \boldsymbol{F} \cdot \boldsymbol{v} dt $$

另一方面，能量 $E(\boldsymbol{k})$ 是波矢 $\boldsymbol{k}$ 的函数，其全微分为：

$$ dE = \nabla_{\boldsymbol{k}} E(\boldsymbol{k}) \cdot d\boldsymbol{k} $$

将速度公式 $\boldsymbol{v} = \frac{1}{\hbar} \nabla_{\boldsymbol{k}} E(\boldsymbol{k})$ 代入上式：

$$ dE = \hbar \boldsymbol{v} \cdot d\boldsymbol{k} $$

对比外力做功公式 $dE = \boldsymbol{F} \cdot \boldsymbol{v} dt$ 和全微分公式，我们可以得到：

$$ \boldsymbol{F} \cdot \boldsymbol{v} dt = \hbar \boldsymbol{v} \cdot d\boldsymbol{k} $$

$$ \boldsymbol{F} = \hbar \frac{d\boldsymbol{k}}{dt} $$

这就是准动量定理。它表明外力等于准动量 $\hbar \boldsymbol{k}$ 的时间变化率，建立了外力与 $\boldsymbol{k}$ 空间演化的直接联系。

有效质量的推导与张量形式

为了将准经典运动与牛顿第二定律 $\boldsymbol{F}=m\boldsymbol{a}$ 类比，我们需要考察电子的加速度。

加速度 $\boldsymbol{a}$ 是速度对时间的导数：

$$ \boldsymbol{a} = \frac{d\boldsymbol{v}}{dt} $$

代入速度公式 $\boldsymbol{v} = \frac{1}{\hbar} \nabla_{\boldsymbol{k}} E(\boldsymbol{k})$：

$$ \boldsymbol{a} = \frac{d}{dt} \left( \frac{1}{\hbar} \nabla_{\boldsymbol{k}} E(\boldsymbol{k}) \right) $$

利用链式法则，将对时间 $t$ 的求导转化为对波矢 $\boldsymbol{k}$ 的求导：

$$ a_\alpha = \frac{d v_\alpha}{dt} = \sum_{\beta} \frac{\partial v_\alpha}{\partial k_\beta} \frac{d k_\beta}{dt} $$

其中 $\alpha, \beta$ 代表坐标轴方向 ($x, y, z$)。将准动量定理 $\frac{d k_\beta}{dt} = \frac{1}{\hbar} F_\beta$ 代入：

$$ a_\alpha = \sum_{\beta} \frac{\partial}{\partial k_\beta} \left( \frac{1}{\hbar} \frac{\partial E}{\partial k_\alpha} \right) \frac{1}{\hbar} F_\beta $$

整理后得到加速度分量的表达式：

$$ a_\alpha = \sum_{\beta} \left( \frac{1}{\hbar^2} \frac{\partial^2 E}{\partial k_\alpha \partial k_\beta} \right) F_\beta $$

为了类比牛顿定律 $\boldsymbol{a} = \boldsymbol{m}^{-1} \boldsymbol{F}$，我们定义倒有效质量张量：

$$ \left( \frac{1}{m^*} \right)_{\alpha\beta} = \frac{1}{\hbar^2} \frac{\partial^2 E}{\partial k_\alpha \partial k_\beta} $$

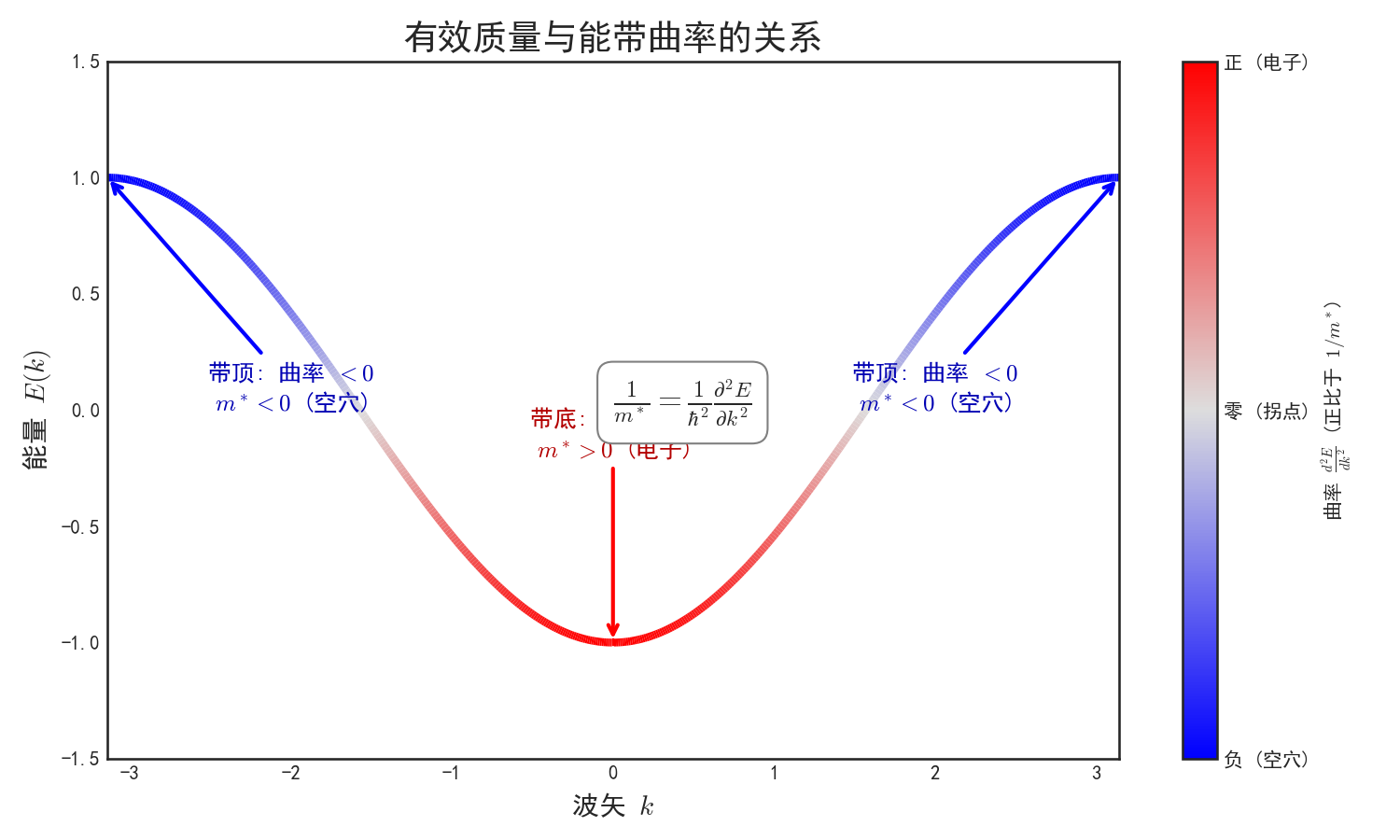
这表明有效质量取决于能带 $E(\boldsymbol{k})$ 的曲率。

展示了有效质量 $m^*$ 与能带二阶导数（曲率）的关系。在带底（曲率>0），有效质量为正；在带顶（曲率<0），有效质量为负（空穴的起源）。通过颜色映射展示质量的变化。

满带不导电的严格证明

电流密度 $\boldsymbol{J}$ 是所有电子速度的加权和。对于一个体积为 $V$ 的晶体：

$$ \boldsymbol{J} = \frac{-e}{V} \sum_{\boldsymbol{k} \in \text{BZ}} \boldsymbol{v}(\boldsymbol{k}) $$

由于能带结构 $E(\boldsymbol{k})$通常具有中心反演对称性（即便晶体没有反演中心，若不考虑自旋轨道耦合，$E(\boldsymbol{k})=E(-\boldsymbol{k})$ 依然成立）：

$$ E(\boldsymbol{k}) = E(-\boldsymbol{k}) $$

速度是能量的梯度，因此：

$$ \boldsymbol{v}(\boldsymbol{k}) = \frac{1}{\hbar} \nabla_{\boldsymbol{k}} E(\boldsymbol{k}) = - \frac{1}{\hbar} \nabla_{-\boldsymbol{k}} E(-\boldsymbol{k}) = - \boldsymbol{v}(-\boldsymbol{k}) $$

对于满带，求和遍历整个布里渊区。由于 $\boldsymbol{v}(\boldsymbol{k})$ 和 $\boldsymbol{v}(-\boldsymbol{k})$ 成对出现且大小相等、方向相反：

$$ \sum_{\boldsymbol{k}} \boldsymbol{v}(\boldsymbol{k}) = 0 $$

$$ \boldsymbol{J}_{\text{满带}} = 0 $$

这就从理论上证明了满带电子对宏观电流无贡献。

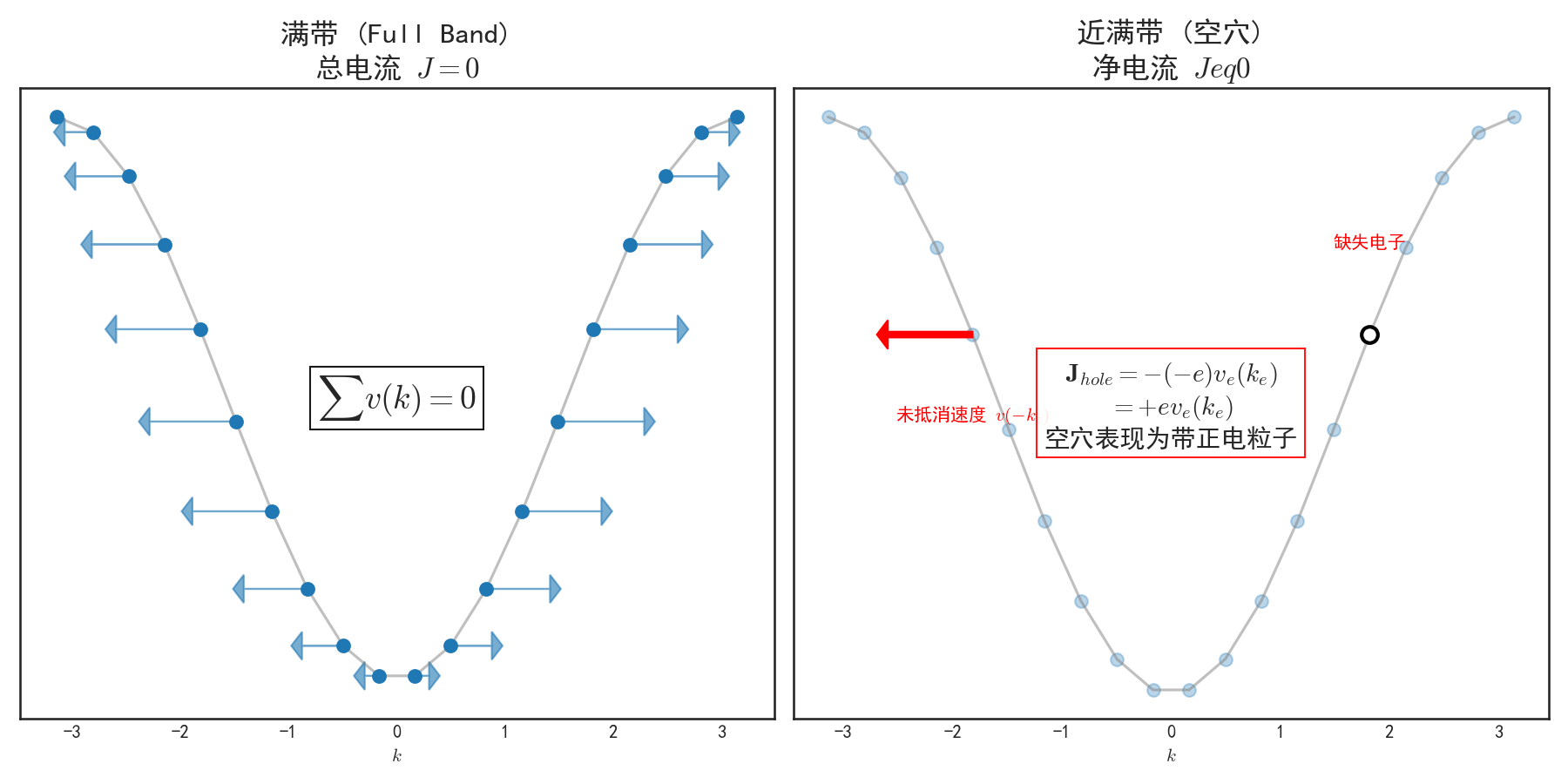
展示了对称性导致电流抵消的原理。
左图：满带情况。每一个 $k$ 态的速度 $v(k)$ 都有一个反向的 $v(-k)$ 抵消，总和为0。
右图：空穴导电。移除了一个电子后，未被抵消的速度导致了净电流，等效为一个带正电的空穴。

空穴概念的定量转化

空穴是描述近满带导电行为的数学技巧。

近满带的总电流等于满带电流减去缺失电子（空状态）的电流：

$$ \boldsymbol{J}_{\text{近满带}} = \boldsymbol{J}_{\text{满带}} - (-e)\boldsymbol{v}_e(\boldsymbol{k}_e) $$

由于 $\boldsymbol{J}_{\text{满带}} = 0$，则：

$$ \boldsymbol{J}_{\text{近满带}} = 0 - (-e)\boldsymbol{v}_e(\boldsymbol{k}_e) $$

$$ \boldsymbol{J}_{\text{空穴}} = +e \boldsymbol{v}_e(\boldsymbol{k}_e) $$

这一定义推导出空穴的三个核心属性：

1. 电荷：$+e$（电子电荷的相反数）。
2. 速度：$\boldsymbol{v}_h = \boldsymbol{v}_e$（空穴速度等于该状态若被占据时的电子速度）。
3. 有效质量：由于能带顶部电子质量 $m^*_e < 0$，根据动力学方程匹配，空穴质量定义为 $m^*_h = -m^*_e > 0$。

恒定磁场中的回旋共振频率

在磁场 $\boldsymbol{B}$ 中，电子受到洛伦兹力（忽略电场）：

$$ \boldsymbol{F} = -e (\boldsymbol{v} \times \boldsymbol{B}) $$

结合动力学方程 $\boldsymbol{F} = m^* \frac{d\boldsymbol{v}}{dt}$（假设各向同性有效质量 $m^*$）：

$$ m^* \frac{d\boldsymbol{v}}{dt} = -e (\boldsymbol{v} \times \boldsymbol{B}) $$

对于垂直于磁场平面的速度分量 $\boldsymbol{v}_\perp$，电子做匀速圆周运动。向心力由洛伦兹力提供：

$$ e v_\perp B = m^* \frac{v_\perp^2}{R} = m^* \omega_c v_\perp $$

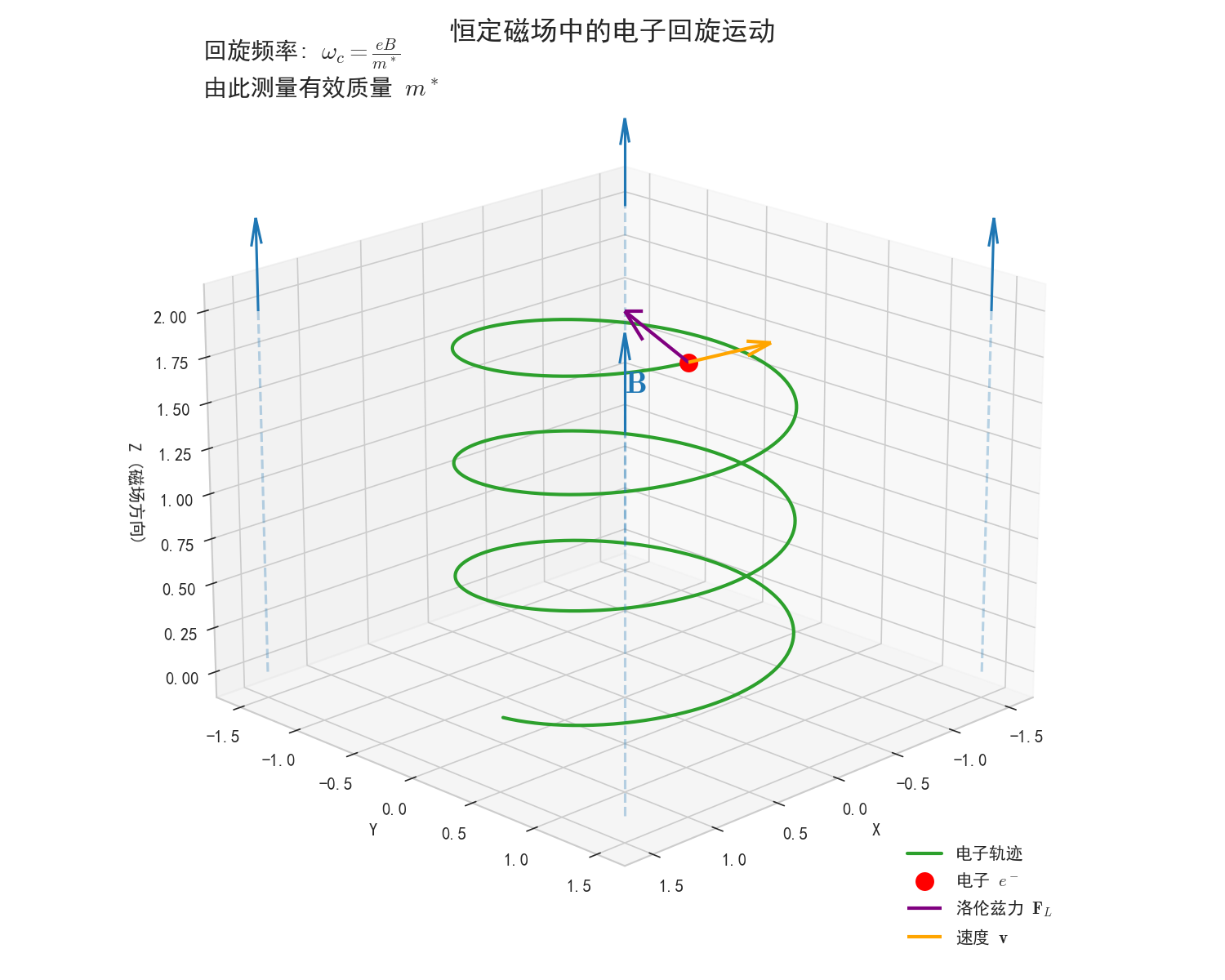
电子在磁场中的螺旋运动，这是回旋共振的物理图像。电子在 $\mathbf{B}$ 场下的洛伦兹力作用下，垂直方向做圆周运动，平行方向匀速运动。

由此得到回旋共振频率 $\omega_c$（Cyclotron Frequency）的标准公式：

$$ \omega_c = \frac{eB}{m^*} $$

在实验中，通过测量共振吸收频率 $\omega_c$ 和已知磁场 $B$，即可反推出材料的有效质量：

$$ m^* = \frac{eB}{\omega_c} $$