例题分析

这些题目不仅仅是计算，更是对理论体系的再一次“复盘”。它们涵盖了从波函数的基本性质，到两种近似模型的具体计算，最后到电子动力学和统计性质的综合应用。

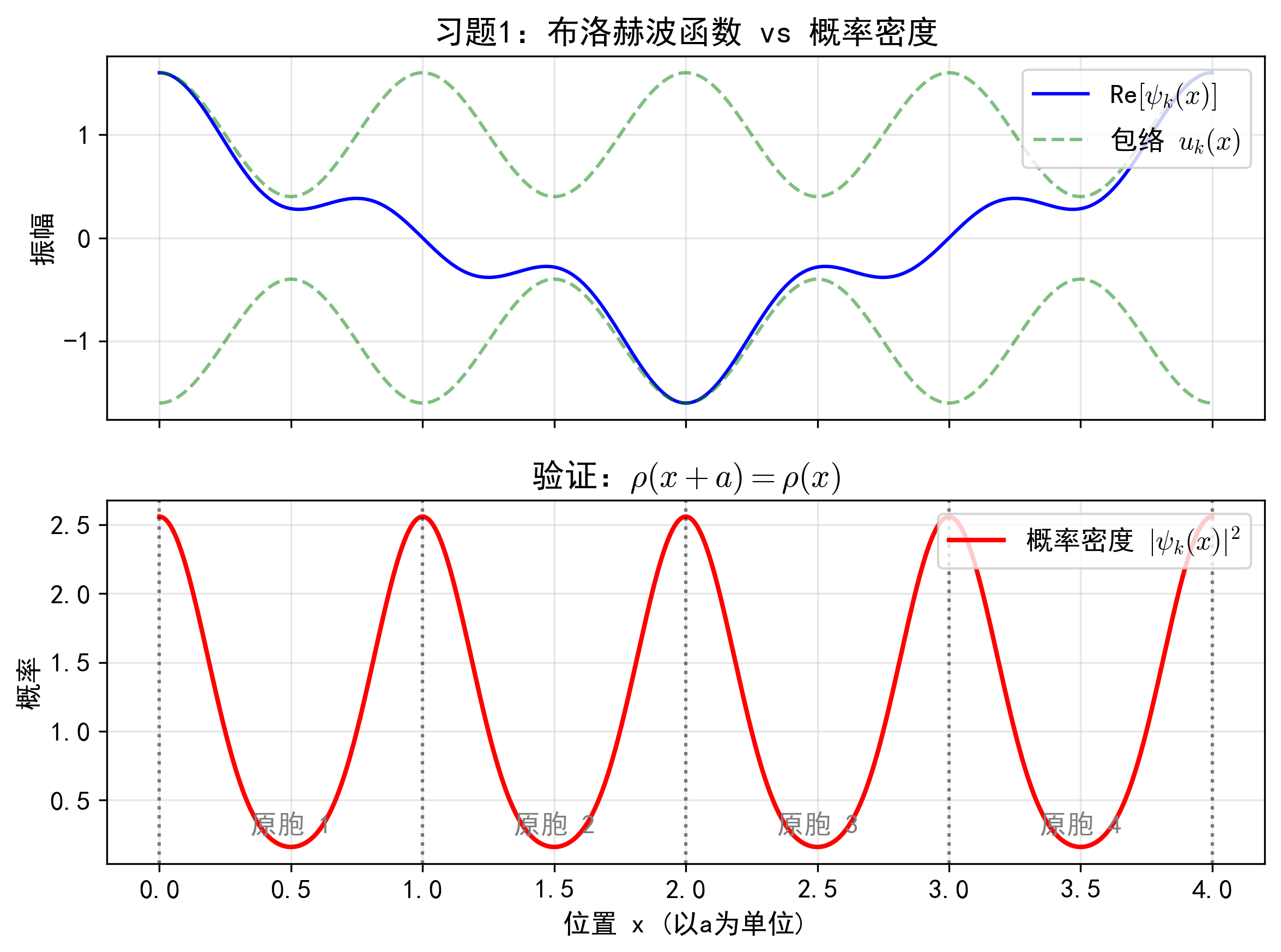
习题 1：布洛赫定理与电子概率密度的周期性

问题
已知一维晶体中电子的布洛赫波函数为 $\psi_k(x) = e^{ikx} u_k(x)$。
(1) 证明电子在晶体中出现的概率密度 $\rho(x)$ 具有与晶格相同的周期性，即 $\rho(x+na) = \rho(x)$。
(2) 如果 $k$ 变为 $k' = k + \frac{2\pi}{a}n$，证明波函数描述的物理状态不变。

知识点
本题对应PPT第6-14页及布洛赫定理推导部分。

• 重点关联：考察布洛赫函数的定义式以及平移算符的物理意义（笔记中强调的 $|\lambda|=1$）。
• 递进关系：这是能带理论的数学基石，理解了波函数的周期性调幅，才能理解后面的微扰计算。

思路

1. 利用布洛赫定理 $\psi(x+a) = e^{ika}\psi(x)$ 或者 $\psi(x) = e^{ikx}u(x)$ 的形式。
2. 概率密度定义为 $\rho(x) = |\psi(x)|^2 = \psi^*(x)\psi(x)$。
3. 利用倒格矢 $G = \frac{2\pi}{a}n$ 的性质 $e^{iGx} = 1$ (在格点处) 或 $u_k$ 的周期性。

解答
(1) 证明概率密度周期性：
根据布洛赫定理，晶体电子波函数满足：
$$ \psi_k(x+a) = e^{ika} \psi_k(x) $$
其中 $a$ 为晶格常数。
电子的概率密度为：
$$ \rho(x+a) = |\psi_k(x+a)|^2 = \psi_k^*(x+a) \psi_k(x+a) $$
代入布洛赫性质：
$$ \rho(x+a) = (e^{-ika} \psi_k^*(x)) (e^{ika} \psi_k(x)) = e^{-ika}e^{ika} \psi_k^*(x)\psi_k(x) $$
因为 $e^{-ika}e^{ika} = 1$，所以：
$$ \rho(x+a) = \psi_k^*(x)\psi_k(x) = \rho(x) $$
这说明电子出现的概率密度具有晶格周期性。

波函数在振荡，但底下的概率密度图是完美重复的，这直接证明了“物理状态的周期性”。

(2) 证明波矢平移等价性：
设 $k' = k + G_n$，其中 $G_n = \frac{2\pi}{a}n$。
布洛赫波函数的一般形式为：
$$ \psi_{k'}(x) = e^{i(k+G_n)x} u_{k'}(x) = e^{ikx} (e^{iG_n x} u_{k'}(x)) $$
由于 $e^{iG_n x}$ 具有晶格周期性（$e^{iG_n(x+a)} = e^{iG_n x} e^{i 2\pi n} = e^{iG_n x}$），我们可以将括号内的部分定义为新的周期函数 $\tilde{u}_k(x) = e^{iG_n x} u_{k'}(x)$。
因此：
$$ \psi_{k'}(x) = e^{ikx} \tilde{u}_k(x) $$
这依然是一个波矢为 $k$ 的布洛赫函数。因此，波矢 $k$ 和 $k+G_n$ 描述的是同一个量子态（或者说可以通过能带指数 $n$ 的重排来对应），这也是为什么我们将 $k$ 限制在第一布里渊区的原因。

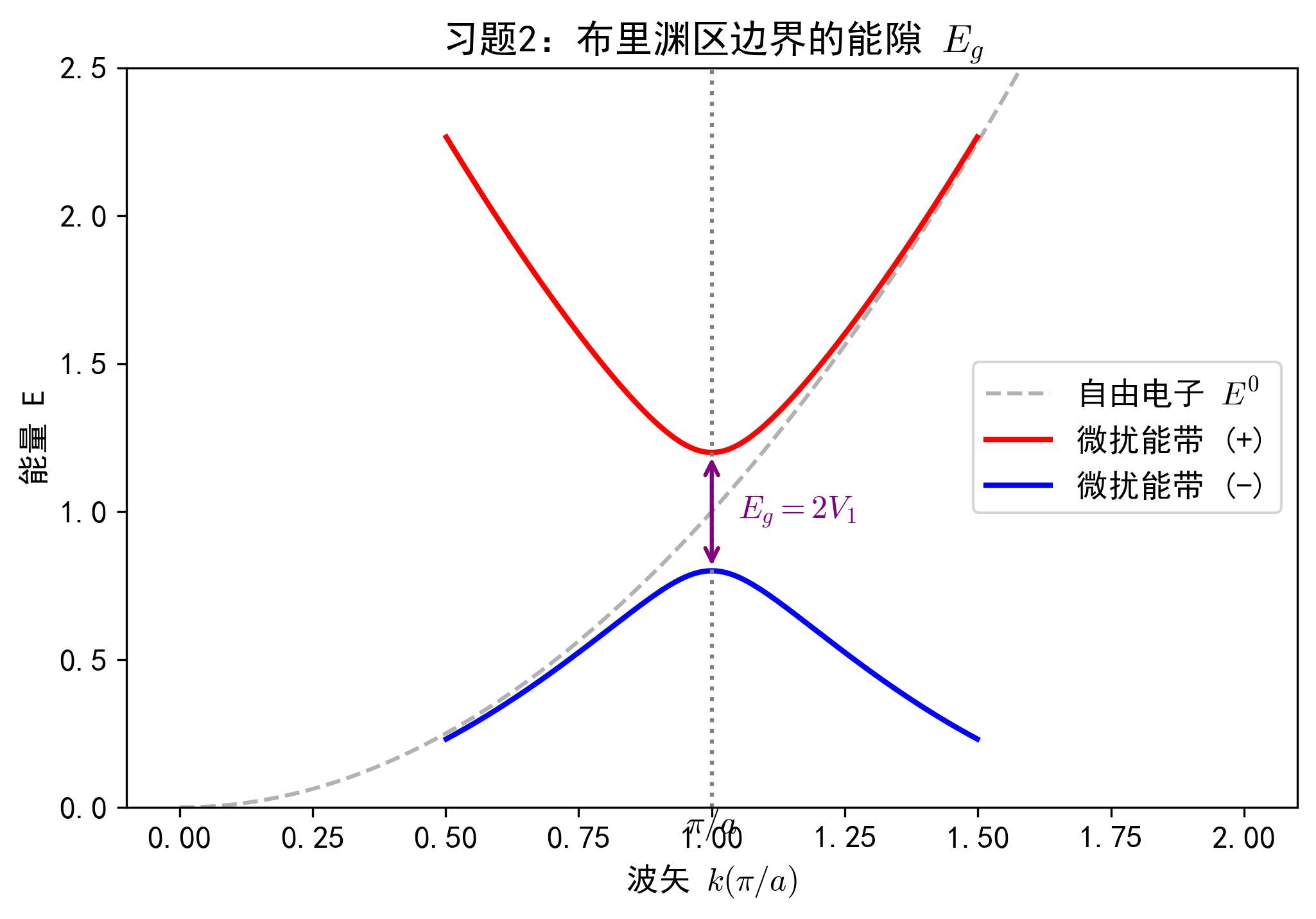
习题 2：近自由电子近似与能隙计算

问题
考虑一维晶格，晶格常数为 $a$。电子受到微弱的周期性势场 $V(x)$ 作用：
$$ V(x) = 2V_1 \cos\left(\frac{2\pi x}{a}\right) $$
(1) 利用简并微扰论，计算在布里渊区边界 $k = \pm \frac{\pi}{a}$ 处的能量本征值。
(2) 求出该处的禁带宽度 $E_g$。

知识点
本题对应PPT第18-35页，特别是笔记中关于“简并微扰”和“能隙形成”的推导。

• 重点关联：PPT强调了在 $k=n\pi/a$ 处，$E^0_k$ 与 $E^0_{k-G}$ 简并，非简并微扰失效，必须解久期方程。
• 递进关系：从定性理解势场对波函数的影响，进阶到定量计算能隙大小。

思路

1. 写出势场的傅里叶展开形式，确定 $V_G$。
2. 确定满足布拉格反射条件的波矢 $k = \pi/a$，此时 $k$ 与 $k' = k - \frac{2\pi}{a} = -\frac{\pi}{a}$ 能量简并。
3. 建立 $2 \times 2$ 的久期方程（Secular Equation）。
4. 求解本征值，差值即为能隙。

解答
(1) 势场的傅里叶展开：
利用欧拉公式，势场可写为：
$$ V(x) = V_1 (e^{i\frac{2\pi}{a}x} + e^{-i\frac{2\pi}{a}x}) $$
对应的倒格矢为 $G = \frac{2\pi}{a}$ 和 $-G = -\frac{2\pi}{a}$。
势场的傅里叶系数为：$V_{G} = V_1, \quad V_{-G} = V_1, \quad V_0 = 0$（假设平均势能为0）。

(2) 建立久期方程：
在边界 $k = \frac{\pi}{a}$ 处，自由电子能量为 $E^0_k = \frac{\hbar^2 (\pi/a)^2}{2m}$。
与之发生强相互作用（简并）的状态是 $k' = k - G = \frac{\pi}{a} - \frac{2\pi}{a} = -\frac{\pi}{a}$。
此时 $E^0_{k'} = \frac{\hbar^2 (-\pi/a)^2}{2m} = E^0_k$。
根据简并微扰论，波函数由 $|\psi_k\rangle$ 和 $|\psi_{k-G}\rangle$ 线性组合而成，系数满足方程组：
$$ \begin{pmatrix} E^0_k - E & V_G \\ V_{-G} & E^0_{k-G} - E \end{pmatrix} \begin{pmatrix} c_1 \\ c_2 \end{pmatrix} = 0 $$
代入数值：
$$ \begin{pmatrix} E^0 - E & V_1 \\ V_1 & E^0 - E \end{pmatrix} = 0 $$

(3) 求解能量与能隙：
令行列式为零：
$$ (E^0 - E)^2 - V_1^2 = 0 $$
$$ E^0 - E = \pm V_1 \implies E = E^0 \pm V_1 $$
即能带在边界处分裂为两个能级：
$$ E_+ = \frac{\hbar^2 \pi^2}{2ma^2} + V_1, \quad E_- = \frac{\hbar^2 \pi^2}{2ma^2} - V_1 $$
禁带宽度为：
$$ E_g = E_+ - E_- = 2V_1 $$
这验证了结论：能隙宽度等于势场相应傅里叶分量幅度的两倍。

红蓝两线在边界分开，中间空出的区域就是禁带。

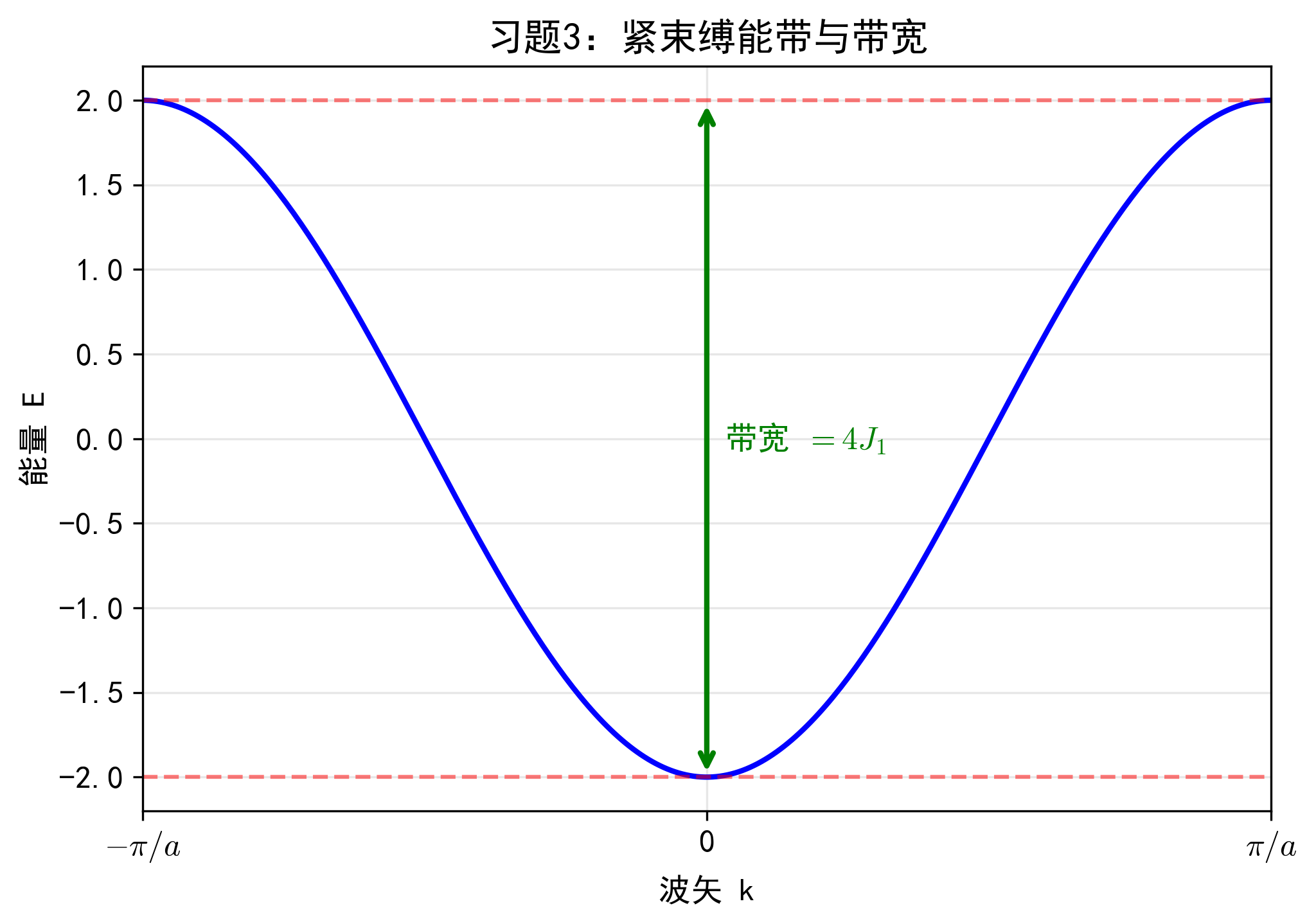
习题 3：紧束缚近似与能带宽度

问题
对于一个晶格常数为 $a$ 的一维单原子链，利用紧束缚近似（只考虑最近邻相互作用），电子的能量色散关系为：
$$ E(k) = E_0 - J_0 - 2J_1 \cos(ka) $$
其中 $E_0$ 为原子能级，$J_1 > 0$ 为最近邻交叠积分。
(1) 画出第一布里渊区内的 $E(k)$ 示意图。
(2) 求出该能带的宽度（Bandwidth）。
(3) 这一结果说明原子间距变小（导致 $J_1$ 变化）时，能带如何变化？

知识点
本题对应PPT第101-120页。

• 重点关联：PPT中详细推导了简单立方晶格的 $s$ 态能带方程。本题将其简化为一维，重点考察对公式物理意义的理解。
• 递进关系：从近自由电子的“微扰断裂”视角，切换到由原子能级“展宽”的视角，这是理解绝缘体和半导体的关键。

思路

1. 分析余弦函数的极值性质。
2. 确定 $k$ 在第一布里渊区 $[-\pi/a, \pi/a]$ 内的最大值和最小值。
3. 能带宽度 = 最大能量 - 最小能量。
4. 联系物理图像：原子靠得越近，波函数重叠越厉害，$J_1$ 越大。

解答

(1) 示意图分析：
函数为余弦函数形式。

• 在 $k=0$ (能带底，$\Gamma$点)：$\cos(0)=1 \Rightarrow E_{min} = E_0 - J_0 - 2J_1$。
• 在 $k=\pm \pi/a$ (能带顶，边界)：$\cos(\pm \pi) = -1 \Rightarrow E_{max} = E_0 - J_0 + 2J_1$。
  图像为开口向上的抛物线形状（在 $k=0$ 附近）。

(2) 能带宽度：
$$ \text{Width} = E_{max} - E_{min} = (E_0 - J_0 + 2J_1) - (E_0 - J_0 - 2J_1) = 4J_1 $$

(3) 物理分析：
$J_1$ 是交叠积分，代表电子在相邻原子间“跳跃”的能力。
当原子间距 $a$ 变小时，相邻原子的波函数重叠程度增加，导致 $J_1$ 增大。
根据 $\text{Width} = 4J_1$，原子间距越小，能带越宽。
这解释了为什么内层电子（重叠小）能带极窄，而外层价电子（重叠大）能带很宽。

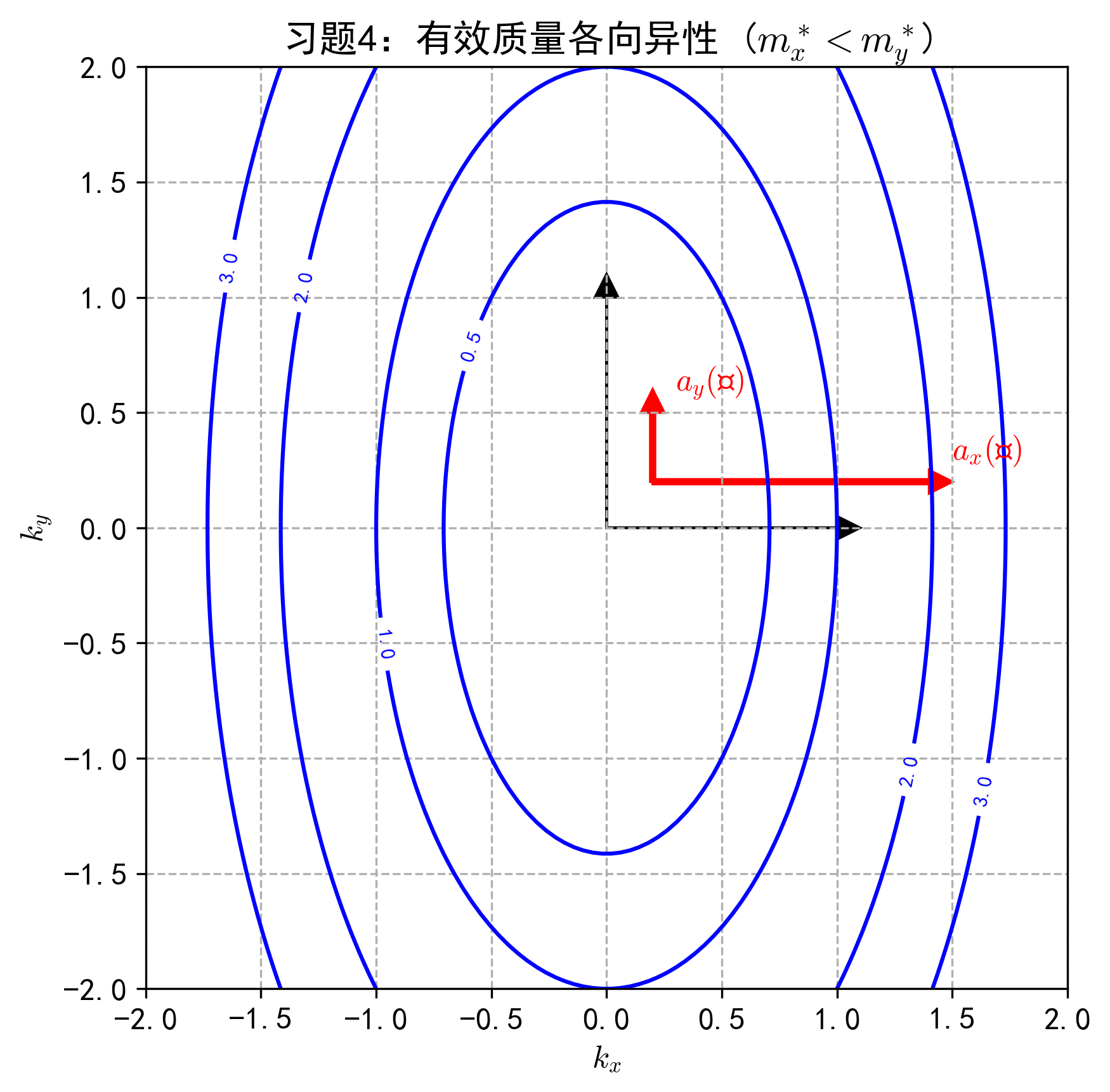
习题 4：有效质量与电子动力学

问题
假设某种二维正方晶格的导带底能量色散关系为：
$$ E(k_x, k_y) = \hbar^2 \left( \frac{k_x^2}{m_1} + \frac{k_y^2}{m_2} \right) $$
其中 $m_1 = m_e, m_2 = 4m_e$ ($m_e$为电子静止质量)。
(1) 求该能带底的有效质量张量。
(2) 如果沿着 $x$ 方向施加恒定电场 $\vec{F} = (F, 0)$，电子的加速度是多少？
(3) 如果沿着 $y$ 方向施加同样的电场，电子的加速度是多少？这说明了什么物理意义？

知识点
本题对应PPT第121-123页及手写笔记中关于曲率与质量关系的讨论。

• 重点关联：有效质量是张量，由二阶导数决定。$m^* = \hbar^2 (\frac{d^2E}{dk^2})^{-1}$。
• 递进关系：将静态的能带结构转化为动态的电子输运性质，理解晶体各向异性。

思路

1. 利用有效质量张量定义 $(m^*)^{-1}_{ij} = \frac{1}{\hbar^2} \frac{\partial^2 E}{\partial k_i \partial k_j}$。
2. 利用准经典运动方程 $\vec{a} = (m^*)^{-1} \vec{F}$。

解答
(1) 有效质量张量：
计算二阶导数：
$$ \frac{\partial^2 E}{\partial k_x^2} = \frac{2\hbar^2}{m_1}, \quad \frac{\partial^2 E}{\partial k_y^2} = \frac{2\hbar^2}{m_2}, \quad \frac{\partial^2 E}{\partial k_x \partial k_y} = 0 $$
倒有效质量张量为：
$$ (\frac{1}{m^*}) = \frac{1}{\hbar^2} \begin{pmatrix} \frac{2\hbar^2}{m_1} & 0 \\ 0 & \frac{2\hbar^2}{m_2} \end{pmatrix} = \begin{pmatrix} \frac{2}{m_1} & 0 \\ 0 & \frac{2}{m_2} \end{pmatrix} $$
注意：题目给出的形式本身已经是泰勒展开形式，通常定义的 $E = \frac{\hbar^2 k^2}{2m^*}$，这里系数没有 $1/2$，所以二阶导数多出了一个因子2。若按照标准定义 $E = \frac{\hbar^2 k_x^2}{2m_x}$，则 $m_x^* = m_1/2$。
这里我们严格按照张量公式计算。

(2) 沿x方向施加电场 $\vec{F} = (F, 0)$：
$$ a_x = (\frac{1}{m^*})_{xx} F_x = \frac{2}{m_1} F = \frac{2F}{m_e} $$
$$ a_y = 0 $$

(3) 沿y方向施加电场 $\vec{F} = (0, F)$：
$$ a_x = 0 $$
$$ a_y = (\frac{1}{m^*})_{yy} F_y = \frac{2}{m_2} F = \frac{2F}{4m_e} = \frac{F}{2m_e} $$

椭圆形的等能面。在x轴方向（椭圆短轴方向），等能面很密，代表曲率大、有效质量小、加速度红箭头很长——这就是“轻电子”。

物理意义：
虽然施加的力大小相同，但电子在 $x$ 方向的加速度是在 $y$ 方向加速度的 4 倍。
这说明晶体中的电子表现出显著的各向异性。能带曲率越大（$x$方向），有效质量越小，电子越容易被加速。

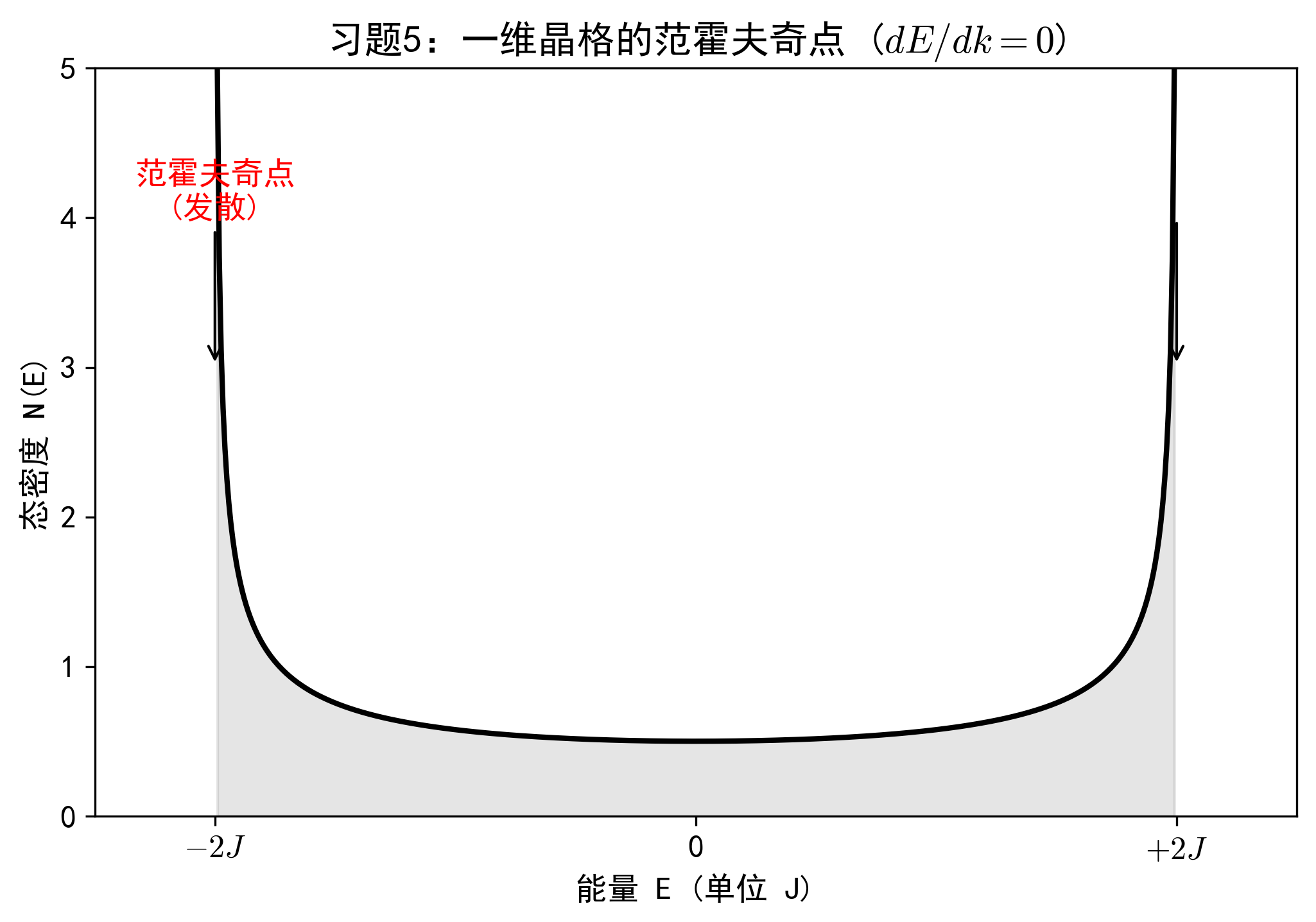
习题 5：能态密度与范霍夫奇点

问题
对于一维紧束缚能带 $E(k) = -2J \cos(ka)$ (忽略常数项)。
(1) 推导一维能态密度 $N(E)$ 的表达式。
(2) 分析当 $E$ 趋近于能带底 ($-2J$) 和能带顶 ($+2J$) 时，$N(E)$ 的变化趋势，并指出奇点类型。

知识点
本题对应PPT第146-155页。

• 重点关联：PPT特别给出了三维情况的积分公式，手写笔记强调了 $dE/dk=0$ 处导致能态密度发散（范霍夫奇点）。
• 递进关系：能态密度是连接微观能级和宏观实验（如X射线发射谱）的桥梁。

思路

1. 利用一维能态密度公式 $N(E) = \frac{2}{\pi} \frac{1}{|dE/dk|}$ (考虑自旋，且 $k$ 空间密度为 $L/\pi$)，或者是单位体积下的 $N(E) = \frac{1}{\pi} \frac{1}{|dE/dk|}$。
2. 计算 $dE/dk$。
3. 利用三角恒等式将 $\sin(ka)$ 转化为 $E$ 的函数。

解答

(1) 推导 $N(E)$：
$$ \frac{dE}{dk} = 2Ja \sin(ka) $$
利用 $\cos(ka) = -E/2J$，有：
$$ \sin(ka) = \sqrt{1 - \cos^2(ka)} = \sqrt{1 - (E/2J)^2} $$
因此：
$$ \left| \frac{dE}{dk} \right| = 2Ja \sqrt{1 - \left(\frac{E}{2J}\right)^2} $$
一维能态密度（不考虑自旋，单位长度）：
$$ N(E) = \frac{1}{\pi} \frac{1}{|dE/dk|} = \frac{1}{2\pi Ja \sqrt{1 - (E/2J)^2}} = \frac{1}{\pi a \sqrt{4J^2 - E^2}} $$

(2) 奇点分析：
当 $E \to \pm 2J$ 时，分母 $\sqrt{4J^2 - E^2} \to 0$。
此时 $N(E) \to \infty$。
这对应于 $dE/dk = 0$ 的点（带顶和带底）。这些点被称为范霍夫奇点 (Van Hove Singularities)。
在一维体系中，能带边缘的态密度是发散的（反比于平方根）。这与三维情况（带边趋于0）形成鲜明对比。

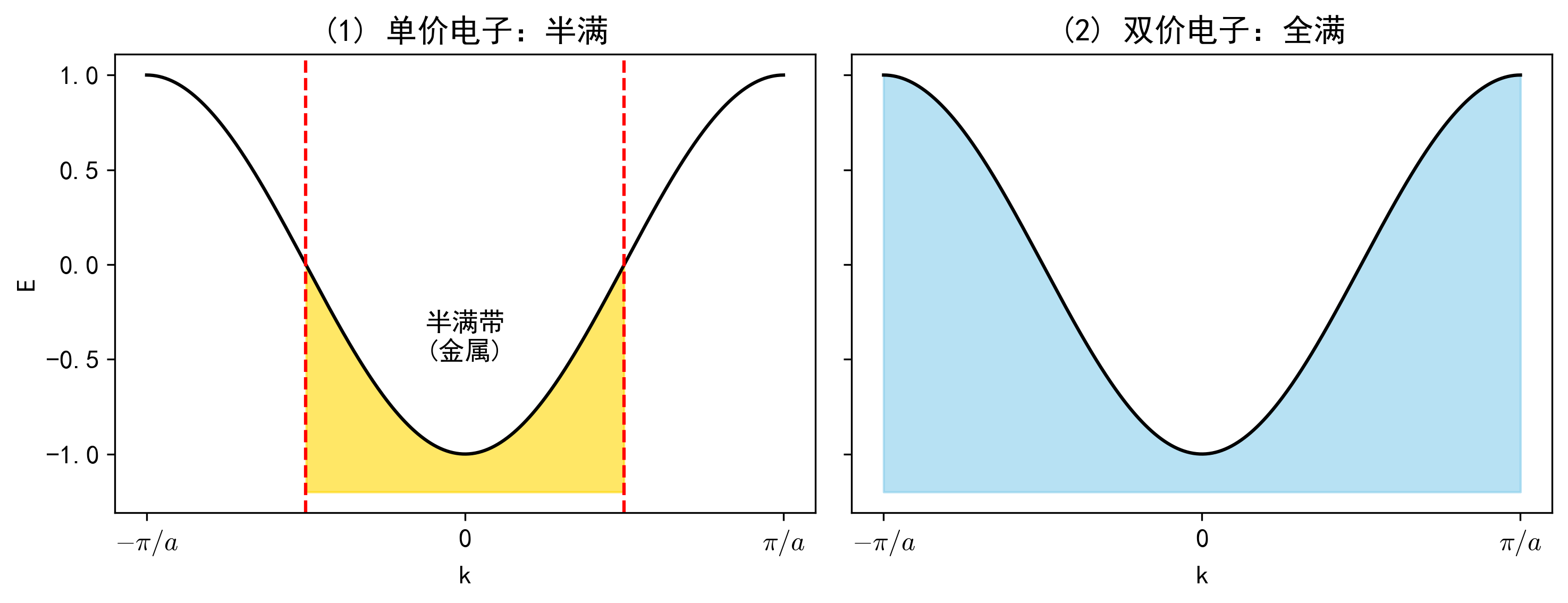
习题 6：能带填充与导电性

问题
考虑一维单原子链，每个原子只有一个价电子。
(1) 按照泡利不相容原理，电子将填充到布里渊区的什么位置？（求费米波矢 $k_F$）。
(2) 此时能带是半满还是全满？该材料是金属还是绝缘体？
(3) 如果原子有两个价电子，情况有何不同？

知识点
本题对应PPT第160-166页及笔记中关于金属/绝缘体判据的讨论。

• 重点关联：PPT明确指出“半满带是金属”，“满带是绝缘体/半导体”。
• 递进关系：这是能带理论的终极应用——解释为什么有的材料导电，有的不导电。

思路

1. 第一布里渊区范围 $[-\pi/a, \pi/a]$，共有 $N$ 个 $k$ 状态。
2. 考虑自旋，每个能带最多容纳 $2N$ 个电子。
3. 根据电子总数判断填充程度。

解答
(1) 费米波矢：
设有 $N$ 个原胞，总长度 $L=Na$。
$k$ 空间状态密度为 $L/2\pi$。
每个原子1个电子，总电子数 $N$。
考虑自旋，每个 $k$ 态容纳2个电子。需要的 $k$ 态数量为 $N/2$。
电子从 $k=0$ 开始向两侧填充，占据的 $k$ 空间长度为：
$$ \Delta k = \frac{N/2}{L/2\pi} = \frac{N\pi}{L} = \frac{N\pi}{Na} = \frac{\pi}{a} $$
填充范围为 $[-\pi/2a, \pi/2a]$。
因此，费米波矢 $k_F = \frac{\pi}{2a}$。

(2) 导电性判定：
第一布里渊区边界为 $\pm \pi/a$。
现在的填充范围是 $\pm \pi/2a$，刚好占据了布里渊区的一半。
结论：这是一个半满带 (Half-filled band)。电子在费米面附近有空的量子态可以跃迁，因此该材料是金属 (导体)。

左边是金色的半满状态（有空位可导电），右边是蓝色的全满状态（无空位不导电）。

(3) 二价原子情况：
如果有2个价电子，总电子数为 $2N$。
需要的状态数为 $2N/2 = N$。
这刚好填满整个第一布里渊区（$2N$个位置全部被占）。
结论：这是一个满带 (Filled band)。

• 如果该能带与更高能带有重叠，它仍是金属（如二价碱土金属）。
• 如果该能带与更高能带之间存在能隙（Gap），且温度较低，它是绝缘体或半导体。

课后习题

【习题一】布洛赫定理的运用

问题

一维周期场中电子的波函数 $\psi_{x}$ 满足 $Bloch$ 定理，若晶格常数为 $a$ 的电子波函数为

$$\psi_{x}=\sin\left ( \frac{\pi x}{a} \right )$$

试求电子在该态的波矢。

知识点

布洛赫定理；一维晶格；傅里叶分解；第一布里渊区。

思路

根据布洛赫定理，电子的波函数可以表示为 $\psi_k(x) = e^{ikx} u_k(x)$，其中 $u_k(x)$ 具有晶格周期性。同时，任何波函数都可以分解为平面波的叠加。将给定的 $\psi(x)$ 转化为复指数形式（平面波），直接读出平面波的波矢 $k$，即为电子在该态的波矢。

解答

根据欧拉公式 $\sin(\theta) = \frac{1}{2i} (e^{i\theta} - e^{-i\theta})$，将给定的波函数 $\psi_{x}$ 展开：

$$\psi_{x} = \sin\left ( \frac{\pi x}{a} \right )$$

$$\psi_{x} = \frac{1}{2i} \left( e^{i\frac{\pi x}{a}} - e^{-i\frac{\pi x}{a}} \right)$$

将上式与布洛赫函数 $\psi_k(x)$ 在近自由电子近似下的平面波展开形式 $\sum_{G} C_{G} e^{i(k-G)x}$ 进行比较。

我们可以将 $\psi_{x}$ 看作是两种平面波的叠加：

$$\psi_{x} \propto e^{i \left(\frac{\pi}{a}\right) x} - e^{i \left(-\frac{\pi}{a}\right) x}$$

因此，该态的波矢 $k$ 为：

$$k = \pm \frac{\pi}{a}$$

结论： 电子在该态的波矢是 $\pm \frac{\pi}{a}$。这两个值对应于一维晶格的第一布里渊区边界上的等价态。

【习题二】布洛赫定理的表述与意义

问题

写出布洛赫定理的表述，尝试进行证明，并简述布洛赫函数的意义。

知识点

布洛赫定理；晶体周期势场；平移对称性；哈密顿量。

思路

1. 清晰表述布洛赫定理的数学形式和文字描述。
2. 证明思路基于晶体哈密顿量 $H$ 与晶格平移算符 $T(\vec{R})$ 对易的性质。
3. 解释布洛赫函数 $u_{\vec{k}}(\vec{r})$ 承担的物理意义。

解答

布洛赫定理表述

布洛赫定理指出，在周期性势场 $V(\vec{r})$ 中运动的电子，其定态薛定谔方程的解 $\psi_{\vec{k}}(\vec{r})$（即电子的波函数）可以表示为一个平面波 $e^{i\vec{k}\cdot\vec{r}}$ 与一个具有晶格周期性的布洛赫函数 $u_{\vec{k}}(\vec{r})$ 的乘积。

$$\psi_{\vec{k}}(\vec{r}) = e^{i\vec{k}\cdot\vec{r}} u_{\vec{k}}(\vec{r})$$

其中，布洛赫函数 $u_{\vec{k}}(\vec{r})$ 满足晶格的周期性：

$$u_{\vec{k}}(\vec{r} + \vec{R}) = u_{\vec{k}}(\vec{r})$$

这里的 $\vec{R}$ 是任意一个布拉伐格子的基矢。

布洛赫定理尝试证明

1. 平移算符与哈密顿量： 晶体的哈密顿量 $H = -\frac{\hbar^2}{2m}\nabla^2 + V(\vec{r})$ 中，势能 $V(\vec{r})$ 具有晶格周期性，即 $V(\vec{r} + \vec{R}) = V(\vec{r})$。定义晶格平移算符 $T(\vec{R})$，满足 $T(\vec{R})\psi(\vec{r}) = \psi(\vec{r}+\vec{R})$。由于势能的周期性，平移算符 $T(\vec{R})$ 与哈密顿量 $H$ 对易：
   $$[H, T(\vec{R})] = 0$$
2. 共同本征函数： 由于 $H$ 和 $T(\vec{R})$ 对易，它们具有一组共同的本征函数。因此，$\psi(\vec{r})$ 既是 $H$ 的本征函数（满足薛定谔方程），也是 $T(\vec{R})$ 的本征函数：
   $$T(\vec{R}) \psi(\vec{r}) = c(\vec{R}) \psi(\vec{r})$$
   即
   $$\psi(\vec{r} + \vec{R}) = c(\vec{R}) \psi(\vec{r})$$
3. 确定本征值： 考虑到两次平移的性质 $T(\vec{R}_1) T(\vec{R}_2) = T(\vec{R}_1 + \vec{R}_2)$，本征值必须满足乘积关系：
   $$c(\vec{R}_1) c(\vec{R}_2) = c(\vec{R}_1 + \vec{R}_2)$$
   该方程的解的形式是指数函数：
   $$c(\vec{R}) = e^{i\vec{k}\cdot\vec{R}}$$
   其中 $\vec{k}$ 是波矢。
4. 最终形式： 将本征值代回，得到：
   $$\psi(\vec{r} + \vec{R}) = e^{i\vec{k}\cdot\vec{R}} \psi(\vec{r})$$
   定义 $u_{\vec{k}}(\vec{r}) = e^{-i\vec{k}\cdot\vec{r}} \psi(\vec{r})$，并检验其周期性：
   $$u_{\vec{k}}(\vec{r} + \vec{R}) = e^{-i\vec{k}\cdot(\vec{r} + \vec{R})} \psi(\vec{r} + \vec{R}) = e^{-i\vec{k}\cdot\vec{r}} e^{-i\vec{k}\cdot\vec{R}} (e^{i\vec{k}\cdot\vec{R}} \psi(\vec{r}))$$
   $$u_{\vec{k}}(\vec{r} + \vec{R}) = e^{-i\vec{k}\cdot\vec{r}} \psi(\vec{r}) = u_{\vec{k}}(\vec{r})$$
   证毕。

布洛赫函数的意义

布洛赫函数 $u_{\vec{k}}(\vec{r})$ 是具有晶格周期性的函数，它描述了电子在每个晶胞内的具体行为和局域化特性。

• 平面波部分 $e^{i\vec{k}\cdot\vec{r}}$ 描述了电子在整个晶体中像自由电子一样传播的特性，其波矢 $\vec{k}$ 决定了电子的宏观动量（或准动量）。
• 布洛赫函数部分 $u_{\vec{k}}(\vec{r})$ 描述了电子受周期性势场调制的特性，体现了电子波在每个晶胞中局域化的振荡行为，即晶体势场对电子运动的周期性散射。

因此，布洛赫函数 $\psi_{\vec{k}}(\vec{r})$ 综合了自由电子的传播性与晶体电子的周期性。

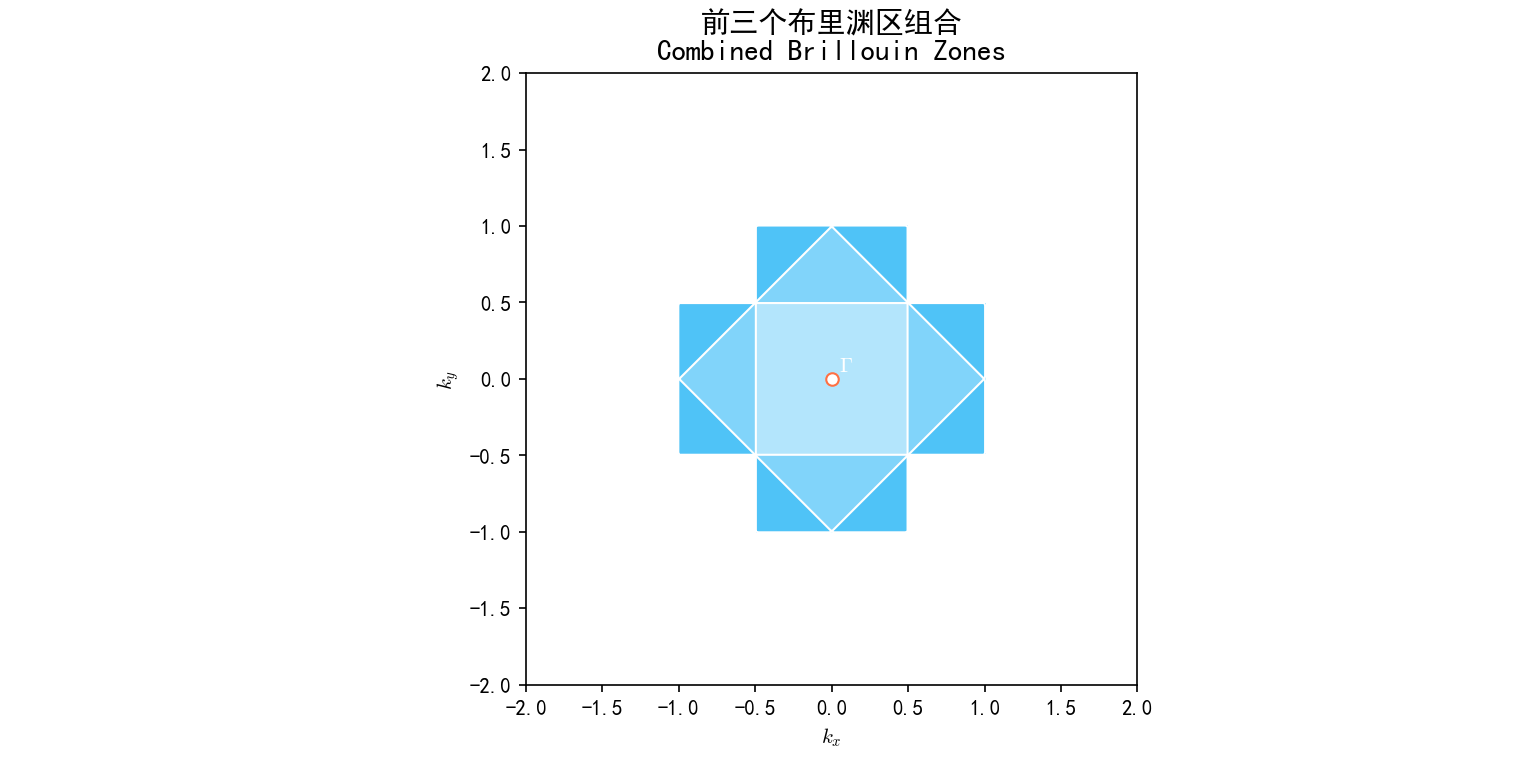
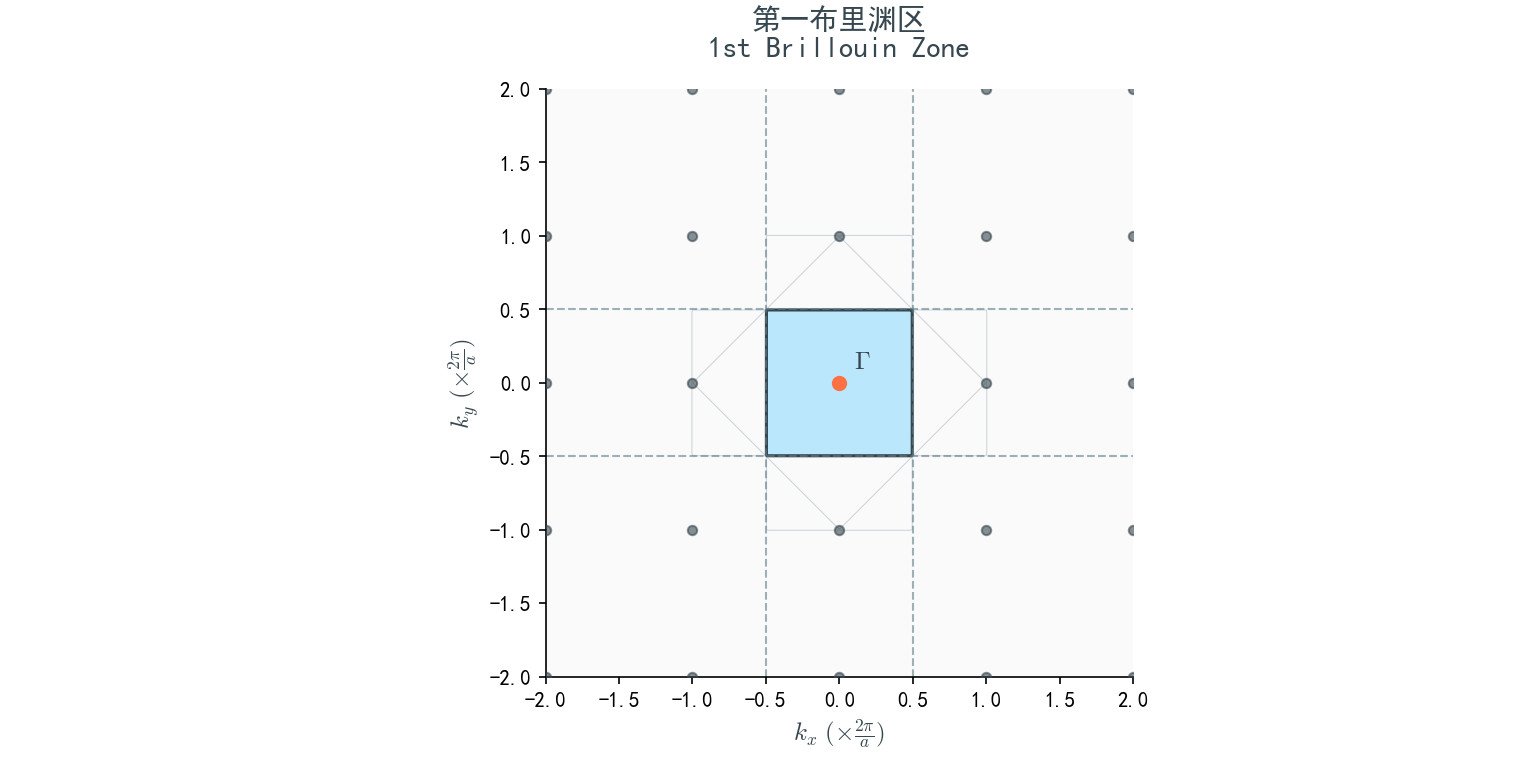
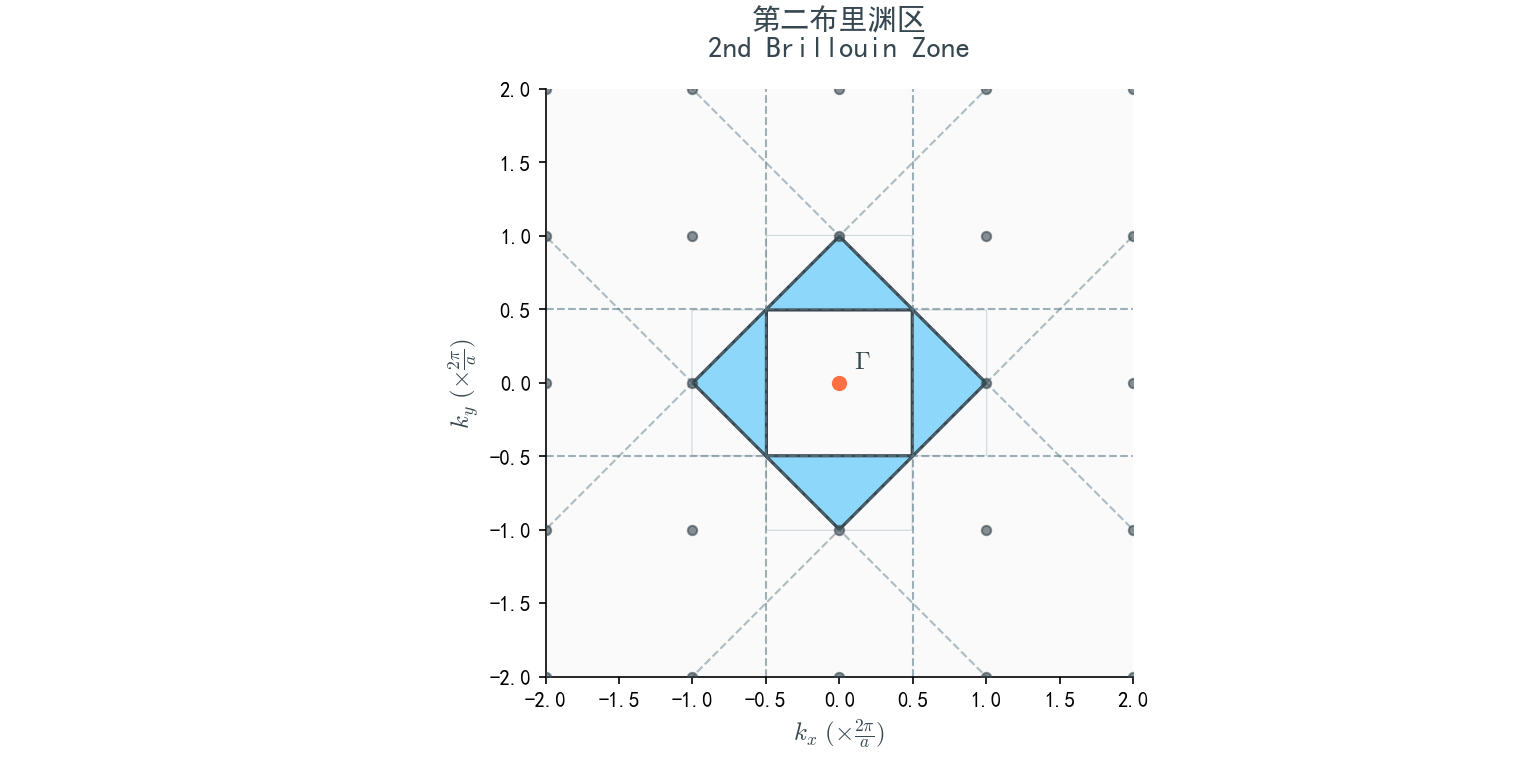
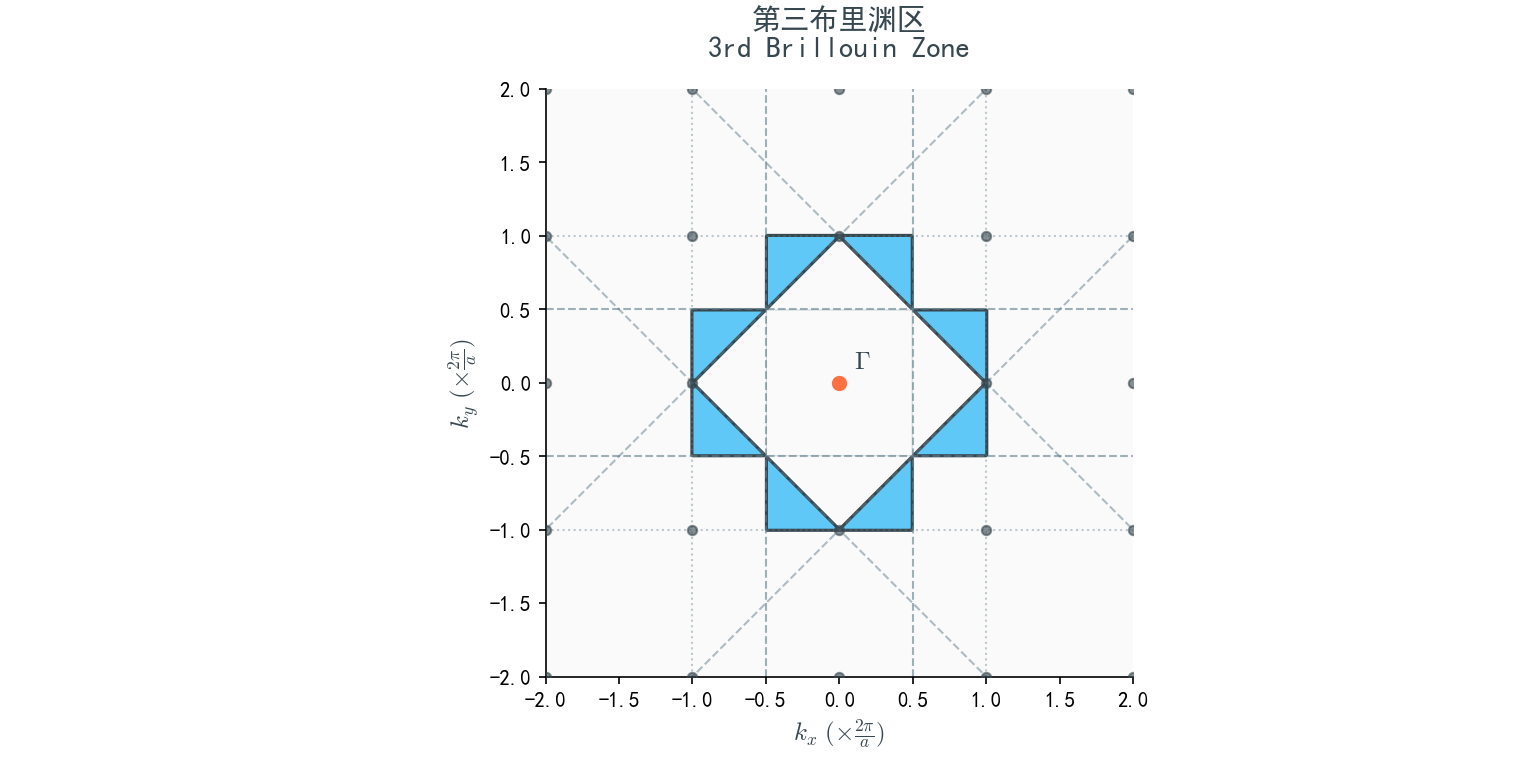
【习题三】二维布里渊区的绘制

问题

绘图表示二维正方格子的第一、 第二、 第三布里渊区并简单说明。

知识点

布里渊区；二维正方格子；倒格子；Wigner-Seitz原胞。

思路

1. 定义二维正方格子的原胞基矢 $\vec{a}_1, \vec{a}_2$ 和倒格子基矢 $\vec{b}_1, \vec{b}_2$。
2. 确定倒格子点 $\vec{G}$ 的位置。
3. 根据布里渊区的定义（倒格子的 Wigner-Seitz 原胞），通过连接原点到各个倒格子点的连线，并作连线的垂直平分线来构造布里渊区。
4. 第一布里渊区由最近邻倒格子点的垂直平分线围成；第二、第三布里渊区由次近邻和更远邻的倒格子点的垂直平分线围成。

解答

二维正方格子参数

设晶格常数为 $a$。

• 原胞基矢：$\vec{a}_1 = a\hat{x}, \vec{a}_2 = a\hat{y}$
• 倒格子基矢：$\vec{b}_1 = \frac{2\pi}{a}\hat{x}, \vec{b}_2 = \frac{2\pi}{a}\hat{y}$
• 倒格子点 $\vec{G}$: $\vec{G} = n_1 \vec{b}_1 + n_2 \vec{b}_2$ ($n_1, n_2$ 为整数)。

布里渊区构造与说明

所有布里渊区都在 $\vec{k}$ 空间（倒格子空间）中构造，以 $\Gamma$ 点 ($\vec{k}=0$) 为中心。

1. 第一布里渊区 (1st BZ)

• 构造： 由连接原点 $\Gamma$ 到最近邻倒格子点（如 $(\pm \frac{2\pi}{a}, 0), (0, \pm \frac{2\pi}{a})$）的连线的垂直平分线围成。
• 几何形状： 以 $\Gamma$ 点为中心，边长为 $\frac{2\pi}{a}$ 的正方形区域。
• 边界定义： $-\frac{\pi}{a} < k_x \le \frac{\pi}{a}$ 且 $-\frac{\pi}{a} < k_y \le \frac{\pi}{a}$。它是倒格子的 Wigner-Seitz 原胞。

2. 第二布里渊区 (2nd BZ)

• 构造： 是紧邻第一布里渊区之外的区域，由连接 $\Gamma$ 点到次近邻倒格子点（如 $(\pm \frac{2\pi}{a}, \pm \frac{2\pi}{a})$）的连线的垂直平分线围成。
• 几何形状： 四个角上的区域（被第一布里渊区的边界切掉的四个三角形区域）。将这四个区域平移（通过倒格子矢量 $\vec{G}$）可以完全填满一个与第一布里渊区面积相等的正方形。
• 边界： $\pm k_x \pm k_y = \pm \frac{2\pi}{a}$。

3. 第三布里渊区 (3rd BZ)

• 构造： 是紧邻第二布里渊区之外的区域，由连接 $\Gamma$ 点到更远的倒格子点（如 $(\pm \frac{2\pi}{a}, 0), (0, \pm \frac{2\pi}{a})$ 的垂直平分线）与第二布里渊区边界共同围成。
• 几何形状： 由八个区域组成，其中四个是位于第一布里渊区四条边中央的区域，四个是位于角上的区域。
• 边界： $-\frac{3\pi}{a} < k_x \le \frac{3\pi}{a}$ 且 $-\frac{3\pi}{a} < k_y \le \frac{3\pi}{a}$ 的范围内，减去第一和第二布里渊区。

【习题四】近自由电子近似

问题

名词解释：近自由电子近似。

知识点

能带理论；周期势场；自由电子模型。

思路

1. 定义该近似的前提条件（势场强度）。
2. 说明该近似的出发点（基态）。
3. 阐述该近似的主要物理结果（能隙）。

解答

近自由电子近似 (Nearly Free Electron Approximation, NFEA) 是能带理论中用于描述晶体中电子运动的一种模型。该模型假设晶体中周期性势场 $V(\vec{r})$ 相对于电子的总动能来说是非常微弱的。因此，可以将电子视为近乎自由，其波函数和能量可从自由电子模型的解出发，将周期势场作为微扰引入。

• 前提： 周期势场 $V(\vec{r})$ 是弱微扰。
• 基本解： 自由电子平面波 $\psi_{\vec{k}}^0(\vec{r}) = A e^{i\vec{k}\cdot\vec{r}}$，能量 $E_{\vec{k}}^0 = \frac{\hbar^2 k^2}{2m}$。
• 核心结果： 弱周期势场对电子能态的影响主要体现在布里渊区边界附近。在边界上，满足布拉格衍射条件 $\vec{k} = \pm \frac{1}{2}\vec{G}$ 的电子波发生反射，形成驻波。由于驻波的波节和波腹相对于原子核的位置不同，导致两种可能的驻波态具有不同的势能平均值，从而在能带结构中打开一个有限的能隙 $\Delta E$，即 $E(\vec{k})$ 曲线在布里渊区边界处是不连续的。

【习题五】一维紧束缚模型与能态密度

问题

有一一维单原子链，间距为 $a$，总长度为 $Na$。
（1）用紧束缚近似方法求出与原子 $s$ 态能级对应的能带的 $E(k)$ 函数；
（2）求出其能态密度函数的表达式；
（3）若每个原子 $s$ 态上只有一个电子，求 $T=0K$ 时的费米能级 $E_{F}^{0}$ 以及 $E_{F}^{0}$ 处的能态密度。

知识点

• 紧束缚近似 (PPT 第101-120页)：重点在于利用 $s$ 态的球对称性和最近邻交叠积分 $J_1$ 推导色散关系。
• 能态密度 (PPT 第146-155页)：重点在于一维情况下范霍夫奇点（Van Hove Singularity）的处理。
• 费米面与能带填充 (PPT 第157-162页)：重点在于利用电子浓度确定费米波矢 $k_F$。

思路

1. 能带推导：从晶体能量期望值公式出发，只考虑最近邻项（$R_m = \pm a$）。
2. 能态密度：利用一维 $N(E)dE = \frac{L}{\pi} dk$ 关系，通过 $dE/dk$ 进行变量代换。
3. 费米能级：根据“一个原子一个电子”判断能带为半满，确定 $k_F$，进而求出能量和态密度。

解答

(1) 求能带函数 $E(k)$

根据紧束缚近似理论，晶体中电子的能量本征值为：
$$ E(k) = E_s - C - \sum_{\vec{R}_m \neq 0} J(\vec{R}_m) e^{i\vec{k}\cdot\vec{R}_m} $$
其中 $E_s$ 为孤立原子s态能级，$C$ 为库仑积分（常数），$J$ 为交叠积分。
在一维原子链中，只考虑最近邻原子的相互作用，最近邻格矢为 $R_m = \pm a$。
假设 $s$ 态波函数具有球对称性，则 $J(a) = J(-a) = J_1$。
代入求和公式：
$$ \begin{aligned} E(k) &= E_s - C - [J_1 e^{ika} + J_1 e^{-ika}] \\ &= E_s - C - 2J_1 \cos(ka) \end{aligned} $$
令能带中心能量为 $E_0 = E_s - C$，则能带表达式为：
$$ E(k) = E_0 - 2J_1 \cos(ka) $$

(2) 求能态密度函数 $N(E)$

一维情况下，长度为 $L=Na$ 的晶体在 $k$ 空间的状态密度为 $\frac{L}{2\pi}$。考虑自旋简并度为 2，则 $k$ 空间单位长度的状态数为 $\frac{L}{\pi}$。
能态密度定义为：
$$ N(E) = \frac{dN}{dE} = \frac{dN}{dk} \left| \frac{dk}{dE} \right| = \frac{L}{\pi} \frac{1}{|dE/dk|} $$
对能带函数求导：
$$ \frac{dE}{dk} = 2J_1 a \sin(ka) $$
利用三角关系 $\sin(ka) = \sqrt{1 - \cos^2(ka)}$，并将 $\cos(ka) = \frac{E_0 - E}{2J_1}$ 代入：
$$ \left| \frac{dE}{dk} \right| = 2J_1 a \sqrt{1 - \left( \frac{E_0 - E}{2J_1} \right)^2} = a \sqrt{4J_1^2 - (E_0 - E)^2} $$
代入能态密度公式：
$$ N(E) = \frac{Na}{\pi} \frac{1}{a \sqrt{4J_1^2 - (E - E_0)^2}} = \frac{N}{\pi \sqrt{4J_1^2 - (E - E_0)^2}} $$
(注：当 $E \to E_0 \pm 2J_1$ 即能带顶和底时，分母趋于0，能态密度发散，这是一维体系特有的范霍夫奇点。)

(3) 求费米能级 $E_F^0$ 和能态密度

确定费米波矢 $k_F$：
每个原子有一个 $s$ 电子，总电子数为 $N$。
根据泡利不相容原理，每个 $k$ 态容纳 2 个电子（自旋向上/向下）。
需要的 $k$ 态数目为 $N/2$。
第一布里渊区范围为 $[-\frac{\pi}{a}, \frac{\pi}{a}]$，总状态数为 $N$。
电子从能带底（$k=0$）开始填充，占据一半的状态，即能带半满。
占据的 $k$ 空间长度为布里渊区长度的一半：
$$ 2k_F = \frac{1}{2} \times \frac{2\pi}{a} \implies k_F = \frac{\pi}{2a} $$

求费米能级 $E_F^0$：
将 $k_F$ 代入能带公式：
$$ E_F^0 = E(k_F) = E_0 - 2J_1 \cos\left( \frac{\pi}{2a} \cdot a \right) = E_0 - 2J_1 \cos\left(\frac{\pi}{2}\right) $$
$$ E_F^0 = E_0 $$
即费米能级位于能带的正中心。

求 $E_F^0$ 处的能态密度：
将 $E = E_F^0 = E_0$ 代入 (2) 中得出的表达式：
$$ N(E_F^0) = \frac{N}{\pi \sqrt{4J_1^2 - (0)^2}} = \frac{N}{2\pi J_1} $$
这表明在能带中心的态密度是有限值，且反比于交叠积分（即反比于带宽）。

【习题六】简单立方晶格与布里渊区几何

问题

（1）证明一个简单立方晶格在第一布里渊区顶角上一个自由电子的动能比该区一边中点大 $2$ 倍。
（2）对一个简单立方晶格，在第一布里渊区顶角上一个自由电子的动能比该区面心上大多少？
（3）说明（2）的结果对 $2$ 价金属的电导有什么影响？

知识点

• 布里渊区几何 (PPT 第90-91页)：简单立方晶格的第一布里渊区是正方体，需掌握高对称点（$\Gamma, X, M, R$）的坐标。
• 近自由电子近似 (PPT 第147-149页)：在远离边界或忽略微扰时，电子能量近似为自由电子动能 $E \propto k^2$。
• 导体与绝缘体判据 (PPT 第164-165页)：能带重叠（Band Overlap）是判断多价金属导电性的关键。

思路

1. 几何坐标：写出简单立方布里渊区各特殊点的坐标。

   • 边长为 $2\pi/a$ 的立方体。
   • 顶角 (Corner, R点)：$k_R = (\frac{\pi}{a}, \frac{\pi}{a}, \frac{\pi}{a})$。
   • 面心 (Face Center, X点)：$k_X = (\frac{\pi}{a}, 0, 0)$（最接近原点的边界点）。
   • 棱边中点 (Edge Center, M点)：$k_M = (\frac{\pi}{a}, \frac{\pi}{a}, 0)$。
   • (注：题目中的“一边中点”根据上下文语境及“大2倍”的数学关系，通常指“面心”，即立方体一个面的中心点；或者指数学上的“边”即棱的中点。我们需要通过计算校验。)
2. 能量计算：利用 $E = \frac{\hbar^2 k^2}{2m}$ 计算各点能量。
3. 物理分析：比较费米球半径 $k_F$ 与布里渊区特征尺寸，判断费米面是否不仅接触边界，还溢出到第二布里渊区。

解答

(1) 证明动能倍数关系

简单立方晶格的第一布里渊区是一个边长为 $\frac{2\pi}{a}$ 的正方体，中心在原点。
顶角（R点）的坐标为：
$$ \vec{k}_R = \left( \frac{\pi}{a}, \frac{\pi}{a}, \frac{\pi}{a} \right) $$
其动能为：
$$ E_R = \frac{\hbar^2}{2m} \left[ \left(\frac{\pi}{a}\right)^2 + \left(\frac{\pi}{a}\right)^2 + \left(\frac{\pi}{a}\right)^2 \right] = \frac{3\hbar^2 \pi^2}{2ma^2} $$

题目中提到的“一边中点”在中文语境下若指布里渊区表面的中心（即面心，X点）：
$$ \vec{k}_X = \left( \frac{\pi}{a}, 0, 0 \right) $$
其动能为：
$$ E_X = \frac{\hbar^2}{2m} \left(\frac{\pi}{a}\right)^2 = \frac{\hbar^2 \pi^2}{2ma^2} $$
比较 $E_R$ 和 $E_X$：
$$ \frac{E_R - E_X}{E_X} = \frac{3 - 1}{1} = 2 $$
即顶角的动能比面心的动能大 2 倍（或者说是其 3 倍）。这与题目描述吻合。
(注：若理解为棱的中点M点，能量为2单位，R为3单位，则是大0.5倍，不符题意。故此处“一边中点”确指面心)

(2) 顶角动能比面心动能大多少

基于上述计算，直接作差：
$$ \Delta E = E_R - E_X = \frac{3\hbar^2 \pi^2}{2ma^2} - \frac{\hbar^2 \pi^2}{2ma^2} = \frac{\hbar^2 \pi^2}{ma^2} $$
即大了一个 $\frac{\hbar^2 \pi^2}{ma^2}$ 的能量单位。

(3) 对 2 价金属电导的影响

电子浓度与费米球：
对于 2 价金属，每个原胞有 2 个价电子。
$k$ 空间状态密度为 $V/(8\pi^3)$，第一布里渊区体积为 $V_{BZ} = (2\pi/a)^3$。
第一布里渊区可容纳的电子数为 $2 \times V_{BZ} \times \frac{V}{(2\pi)^3} / V = 2$ 个电子（考虑自旋）。
这意味着 2 个电子恰好能填满第一布里渊区的所有状态。

能带重叠分析：
如果晶体势场极强，能带之间有禁带，则第一能带全满，第二能带全空，材料应为绝缘体。
但是，根据 (2) 的计算结果，第一布里渊区形状（正方体）各向异性极强：

• 第一能带在面心（X点）处的能量较低（$E \propto 1$）。
• 第一能带在顶角（R点）处的能量很高（$E \propto 3$）。
  对于自由电子气，费米球半径 $k_F$ 由 $n=2/a^3$ 决定：
  $$ k_F = (3\pi^2 n)^{1/3} = \left(\frac{6}{\pi}\right)^{1/3} \frac{\pi}{a} \approx 1.24 \frac{\pi}{a} $$
  注意到：
  $$ k_X = 1.0 \frac{\pi}{a} < k_F < k_R \approx 1.73 \frac{\pi}{a} $$
  这意味着费米球已经超出了第一布里渊区的边界（面心处），但在角顶处还未填满。

结论：
由于第一布里渊区顶角能量（$E_R$）远高于面心能量（$E_X$），导致第一能带的最高能级高于第二能带的最低能级（通常位于第二布里渊区的面心附近）。
这种能带重叠 (Band Overlap) 使得电子会流向第二能带。结果是：

1. 第一能带未填满（角顶空着，有空穴）。
2. 第二能带被部分填充（面心处有电子）。
   因此，尽管是偶数价电子，费米面穿过了能带，材料表现为良导体（金属）。