概念总结与梳理

一、对称性与布洛赫定理

物理逻辑起点：单电子近似与周期性

为了解决多体问题，我们首先引入单电子近似，将复杂的电子-电子相互作用简化为每个电子在平均势场中运动。对于理想晶体，势场 $V(\vec{r})$ 具有严格的晶格周期性。

$$ V(\vec{r} + \vec{R}_n) = V(\vec{r}) $$

晶体中单电子薛定谔方程为：

$$ \hat{H} \psi(\vec{r}) = \left[ -\frac{\hbar^2}{2m}\nabla^2 + V(\vec{r}) \right] \psi(\vec{r}) = E \psi(\vec{r}) $$

平移算符与对易关系

定义平移算符 $\hat{T}_{\vec{R}_n}$，其作用是将波函数平移 $\vec{R}_n$：

$$ \hat{T}_{\vec{R}_n} \psi(\vec{r}) = \psi(\vec{r} + \vec{R}_n) $$

由于势场和动能算符都具有平移不变性，哈密顿量在平移操作下保持不变：

$$ [\hat{H}, \hat{T}_{\vec{R}_n}] = 0 $$

根据量子力学基本原理，对易算符具有共同的本征函数。设 $\psi(\vec{r})$ 同时是 $\hat{H}$ 和 $\hat{T}_{\vec{R}_n}$ 的本征态，对应的平移本征值为 $\lambda_{\vec{R}_n}$。

布洛赫定理的推导

由于波函数在无限晶体中必须有界，本征值的模必须为1，且需满足平移群的乘法性质，因此本征值必须具有指数形式：

$$ \hat{T}_{\vec{R}_n} \psi(\vec{r}) = e^{i\vec{k}\cdot\vec{R}_n} \psi(\vec{r}) $$

这里引入了新的量子数 $\vec{k}$，称为简约波矢。这直接导出了布洛赫定理：

$$ \psi_{\vec{k}}(\vec{r}) = e^{i\vec{k}\cdot\vec{r}} u_{\vec{k}}(\vec{r}) $$

其中 $u_{\vec{k}}(\vec{r})$ 是具有晶格周期性的函数：

$$ u_{\vec{k}}(\vec{r} + \vec{R}_n) = u_{\vec{k}}(\vec{r}) $$

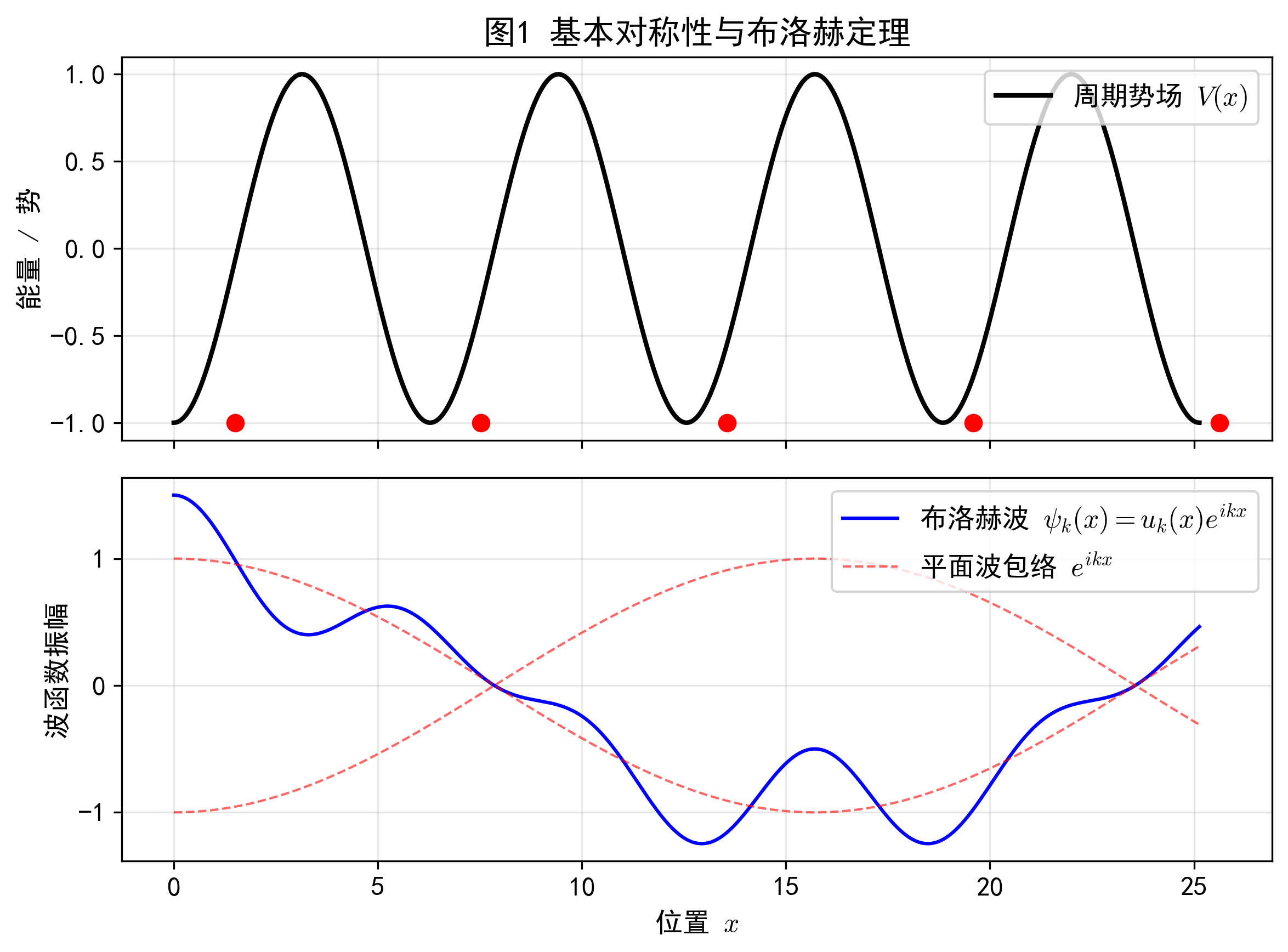
物理意义：晶体电子不是被束缚在某个原子上的，而是共有化的，以调幅平面波的形式在整个晶体中运动。

上半部分显示周期性的原子势场，下半部分展示了被调制的波函数（包络+快速振荡），直观展示“共有化”概念。

二、倒易空间与布里渊区

倒格子的引入

为了描述周期性势场和波矢 $\vec{k}$，引入倒格子基矢 $\vec{b}_i$，满足：

$$ \vec{a}_i \cdot \vec{b}_j = 2\pi \delta_{ij} $$

任意倒格矢 $\vec{G}$ 可以表示为：

$$ \vec{G} = n_1\vec{b}_1 + n_2\vec{b}_2 + n_3\vec{b}_3 $$

布里渊区的定义

由于 $e^{i(\vec{k}+\vec{G})\cdot\vec{R}_n} = e^{i\vec{k}\cdot\vec{R}_n}$，波矢 $\vec{k}$ 和 $\vec{k}+\vec{G}$ 描述的是同一个物理状态。为了避免冗余，我们将 $\vec{k}$ 限制在第一布里渊区内。

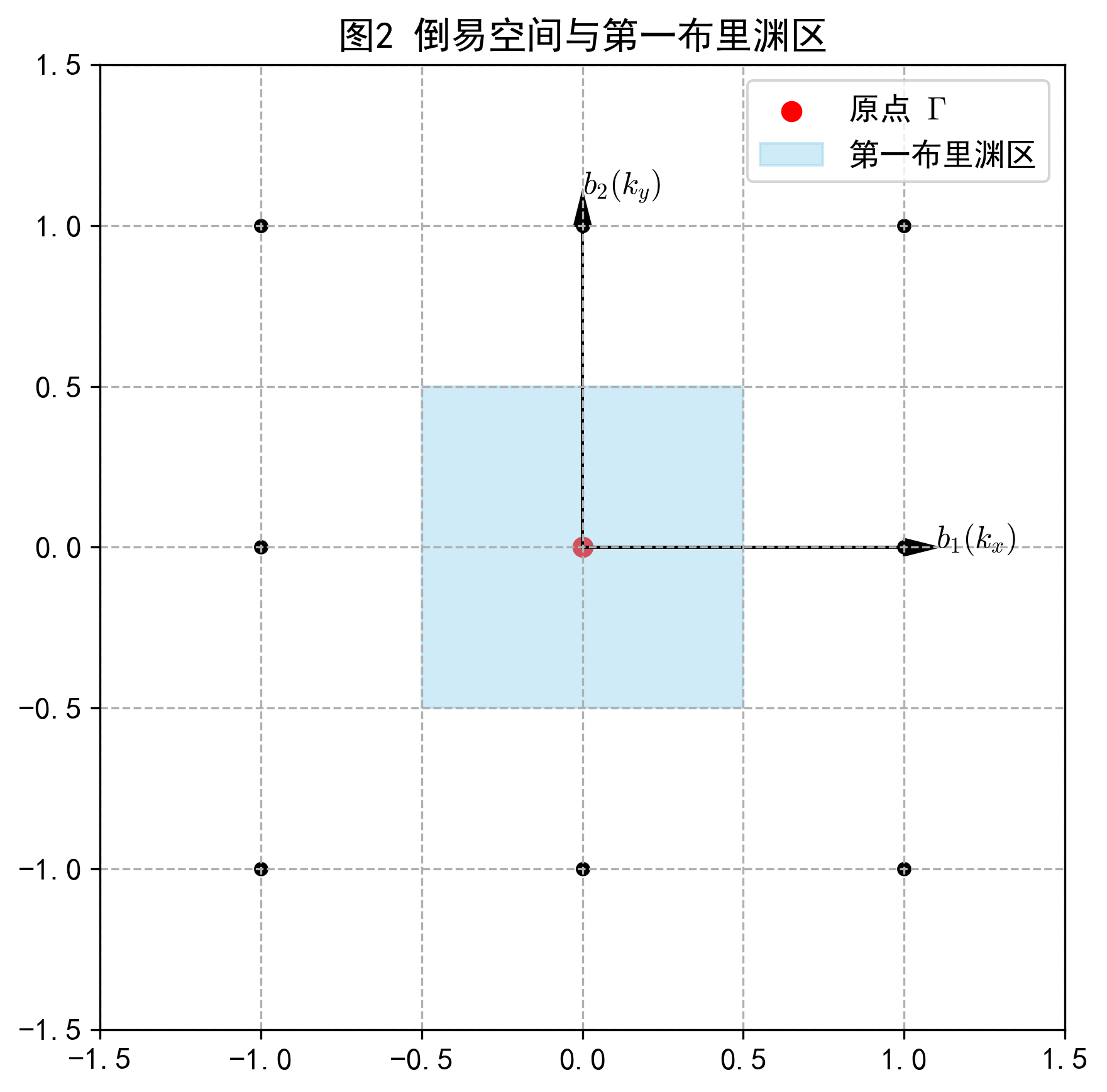
第一布里渊区是倒易空间中的维格纳-赛兹（Wigner-Seitz）原胞，由倒易空间原点到最近邻倒格点连线的垂直平分面围成。它是分析能带结构的几何基础。

清晰的2D倒格点阵列，红色高亮的维格纳-赛兹原胞（第一布里渊区），以及基矢标注。

三、弱场极限——近自由电子近似

物理假设与微扰

适用于简单金属（如碱金属）。假设晶格势场 $V(\vec{r})$ 很弱，作为微扰处理。零级近似为自由电子，能带是抛物线。

$$ E^0(\vec{k}) = \frac{\hbar^2 k^2}{2m} $$

势场展开为傅里叶级数：

$$ V(\vec{r}) = \sum_{\vec{G}} V_{\vec{G}} e^{i\vec{G}\cdot\vec{r}} $$

能隙的形成：简并微扰

当电子波矢 $\vec{k}$ 接近布里渊区边界时，满足布拉格反射条件：

$$ (\vec{k} - \vec{G})^2 \approx k^2 $$

此时，态 $|\vec{k}\rangle$ 和态 $|\vec{k}-\vec{G}\rangle$ 能量简并，非简并微扰论失效。必须使用简并微扰论求解久期方程：

$$ \begin{vmatrix} E^0(\vec{k}) - E & V_{\vec{G}} \\ V_{\vec{G}}^* & E^0(\vec{k}-\vec{G}) - E \end{vmatrix} = 0 $$

解得能量本征值分裂为两支：

$$ E_{\pm} = \frac{1}{2} \left[ E^0(\vec{k}) + E^0(\vec{k}-\vec{G}) \right] \pm \sqrt{\left(\frac{E^0(\vec{k}) - E^0(\vec{k}-\vec{G})}{2}\right)^2 + |V_{\vec{G}}|^2} $$

在布里渊区边界处，能量差（禁带宽度）为：

$$ E_g = 2|V_{\vec{G}}| $$

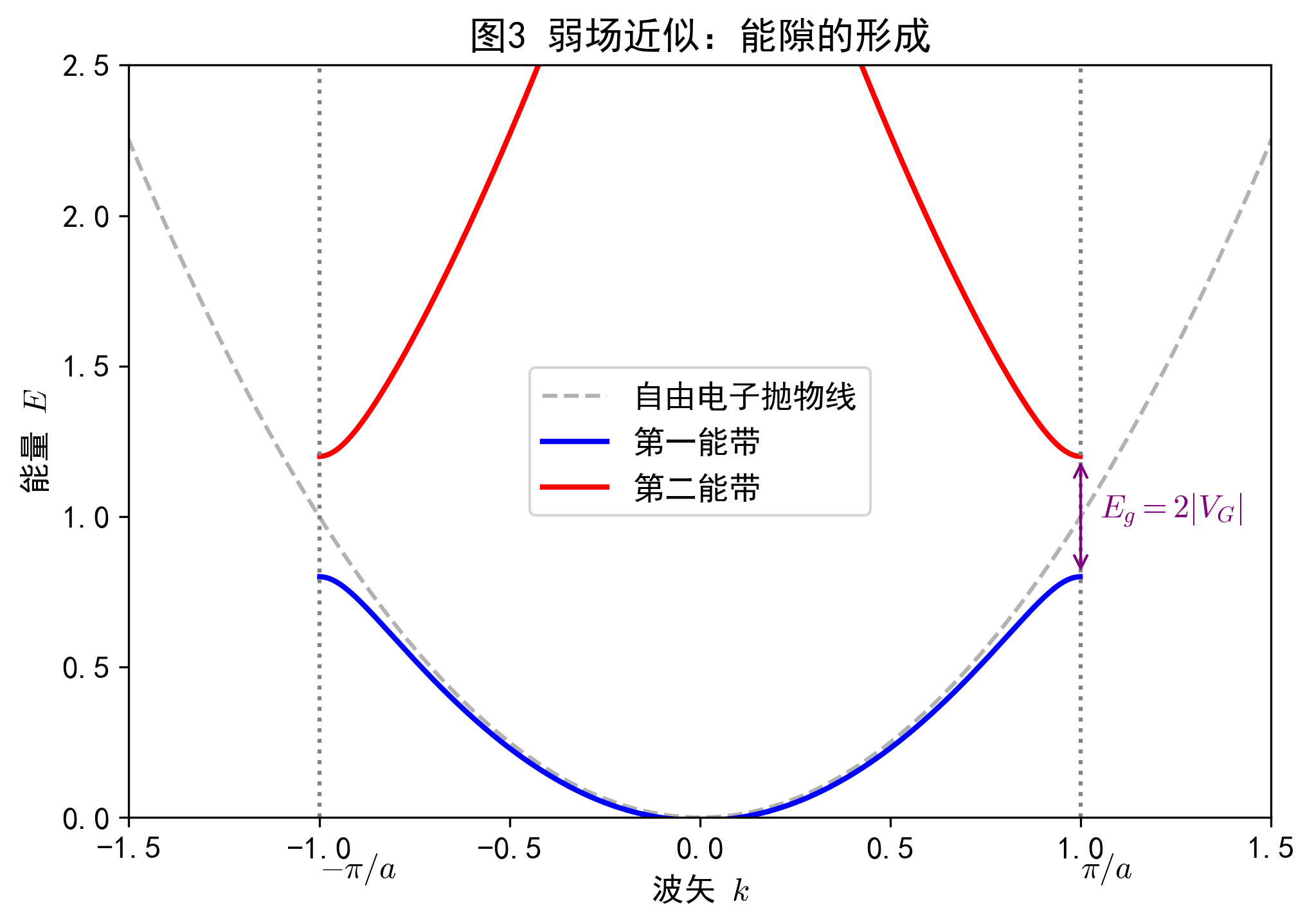
结论：周期性势场的微扰导致能带在布里渊区边界断开，形成能隙。

展示抛物线能带在 $\pm \pi/a$ 处断开，形成 $E_g$ 能隙，直观对应微扰论结果。

四、强场极限——紧束缚近似 (LCAO)

物理假设与线性组合

适用于绝缘体、半导体。假设电子主要被束缚在原子核周围，晶体波函数由孤立原子的原子轨道 $\phi(\vec{r})$ 线性叠加而成。

构造满足布洛赫定理的试探波函数（布洛赫和）：

$$ \psi_{\vec{k}}(\vec{r}) = \frac{1}{\sqrt{N}} \sum_{\vec{R}_n} e^{i\vec{k}\cdot\vec{R}_n} \phi(\vec{r} - \vec{R}_n) $$

能量色散关系

计算能量期望值 $E(\vec{k}) = \langle \psi_{\vec{k}} | \hat{H} | \psi_{\vec{k}} \rangle$。对于简单立方晶格 $s$ 态电子，只考虑最近邻相互作用，能带公式为：

$$ E(\vec{k}) = E_0 - C - 2J (\cos k_x a + \cos k_y a + \cos k_z a) $$

其中 $E_0$ 是原子能级，$C$ 是库仑积分（能级位移），$J$ 是交叠积分（决定带宽）。

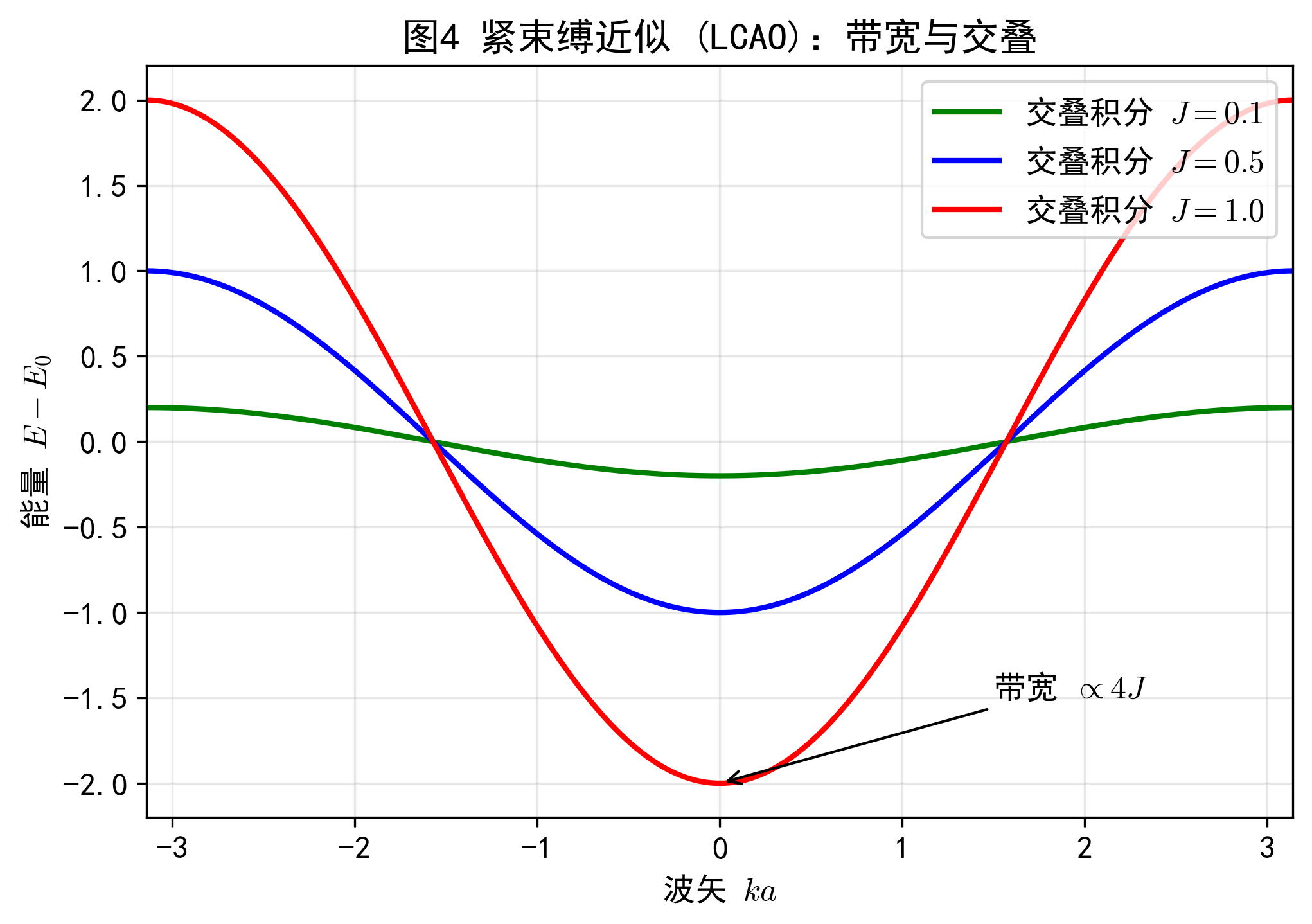
结论：随着原子间距减小，交叠积分 $J$ 增大，孤立的原子能级展宽成能带。能带宽度正比于 $J$。

余弦形式的能带图，不同颜色的线代表不同的交叠积分 $J$，展示 $J$ 越大带越宽的物理图像。

五、电子动力学与有效质量

准粒子概念

为了在半经典近似下描述晶体电子在外场（如电场）下的运动，将晶格势场的复杂作用折叠进电子的质量中，引入有效质量 $m^*$。

有效质量张量

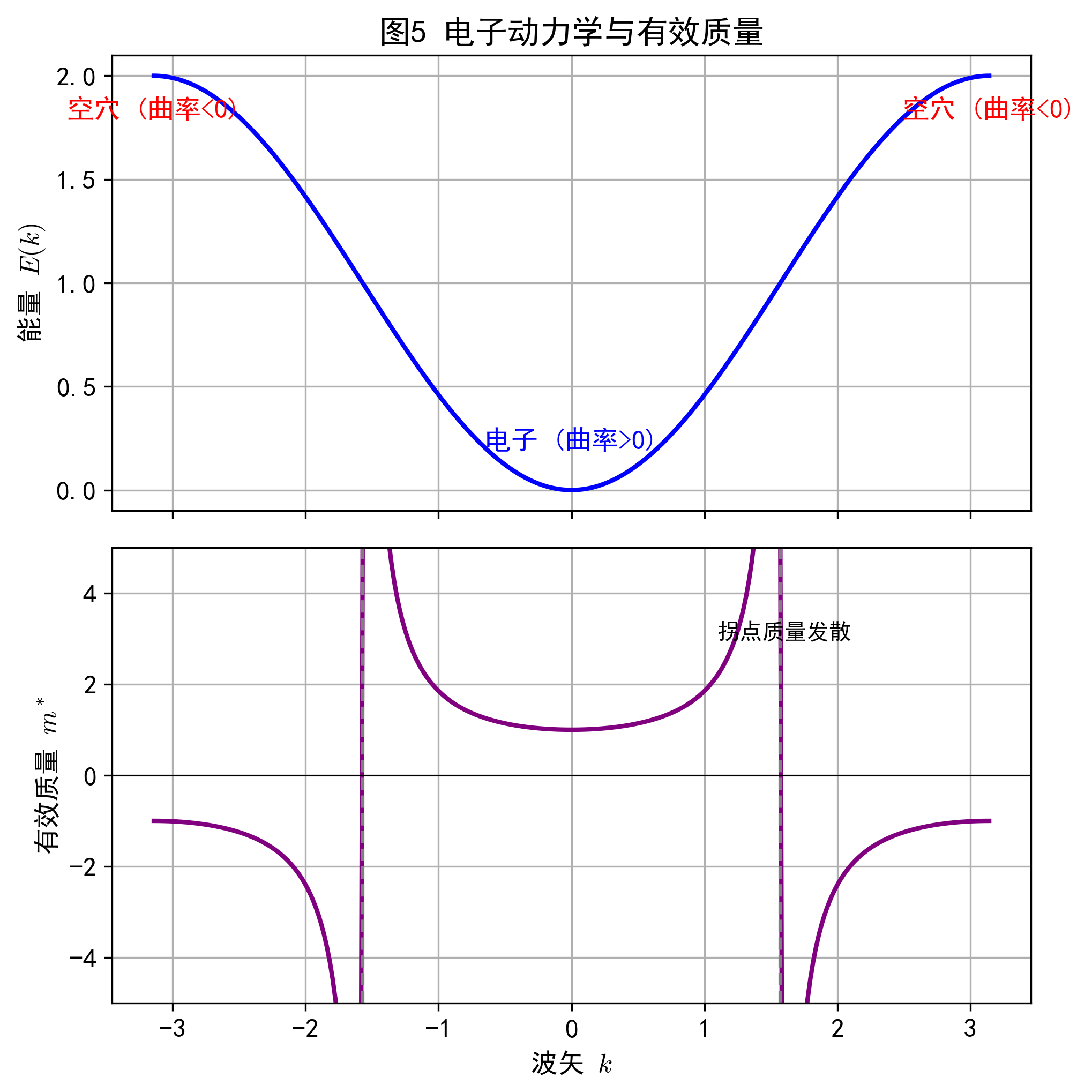
根据群速度 $v_g = \frac{1}{\hbar}\nabla_{\vec{k}}E$ 和外力做功原理，有效质量定义为能带曲率的倒数：

$$ (m^*)^{-1}_{ij} = \frac{1}{\hbar^2} \frac{\partial^2 E}{\partial k_i \partial k_j} $$

• 能带底部：曲率向上，$m^* > 0$，电子行为。
• 能带顶部：曲率向下，$m^* < 0$，表现为带正电的空穴。

上图是能带，下图是有效质量。清楚地看到在能带底质量为正，能带顶质量为负，拐点处质量发散。

六、局域化描述——旺尼尔函数

布洛赫与旺尼尔的对偶

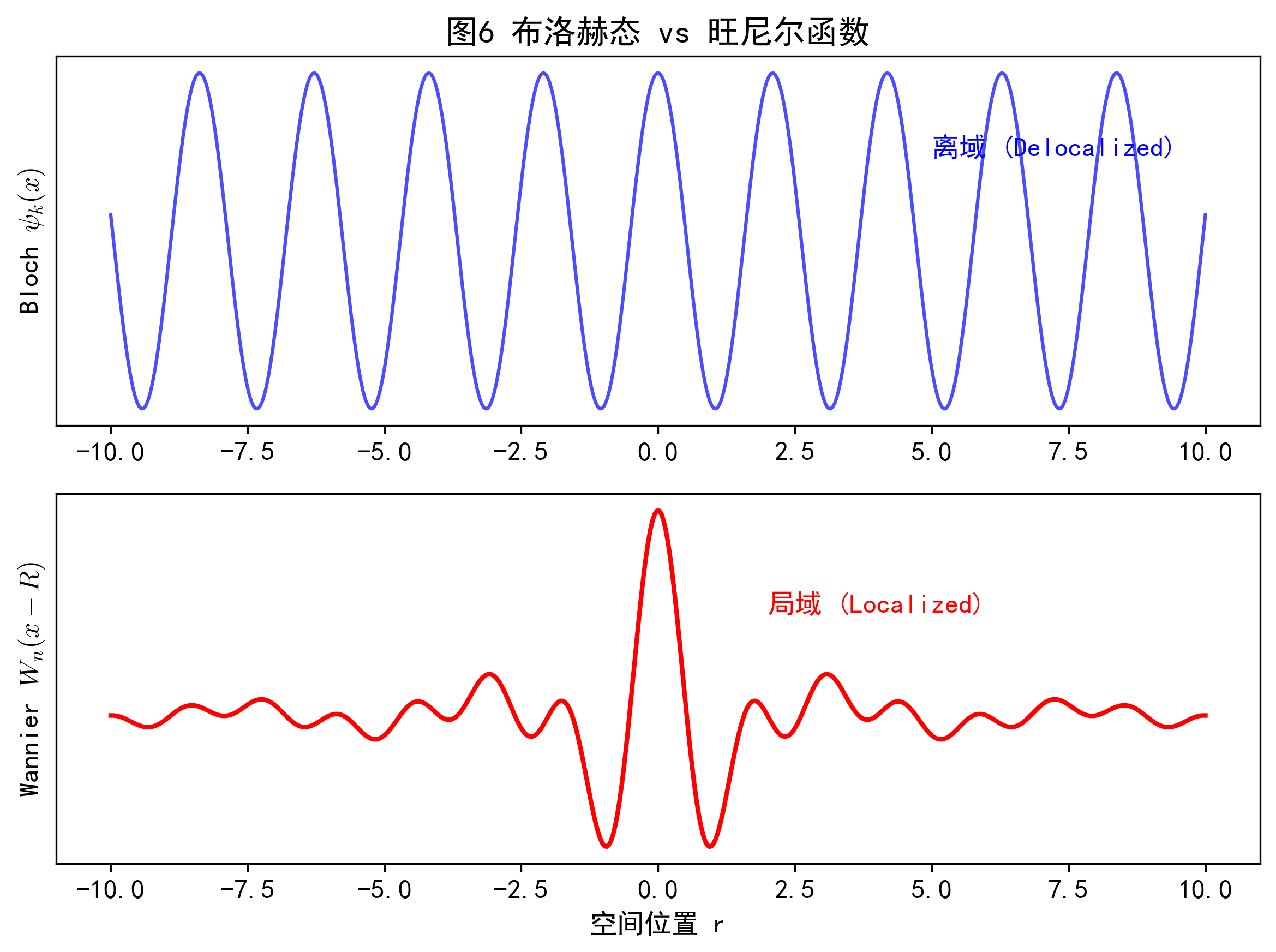
布洛赫函数 $\psi_{\vec{k}}$ 是动量确定的离域态，而旺尼尔函数 $W_n(\vec{r}-\vec{R}_m)$ 是位置确定的局域态。二者通过傅里叶变换联系：

$$ W_n(\vec{r} - \vec{R}_m) = \frac{1}{\sqrt{N}} \sum_{\vec{k}} e^{-i\vec{k}\cdot\vec{R}_m} \psi_{n\vec{k}}(\vec{r}) $$

旺尼尔函数正交归一，是紧束缚近似的严格数学基础，适合处理缺陷、杂质等局域问题。

蓝色波形充满全空间（Bloch），红色波形局域在某一点（Wannier），形成鲜明对比。

七、统计物理——能态密度与费米面

能态密度 (DOS)

定义 $N(E)$ 为单位能量间隔内的量子态数目。利用 $k$ 空间状态均匀分布性质：

$$ N(E) = \frac{V}{4\pi^3} \int_{S_E} \frac{dS}{|\nabla_{\vec{k}} E|} $$

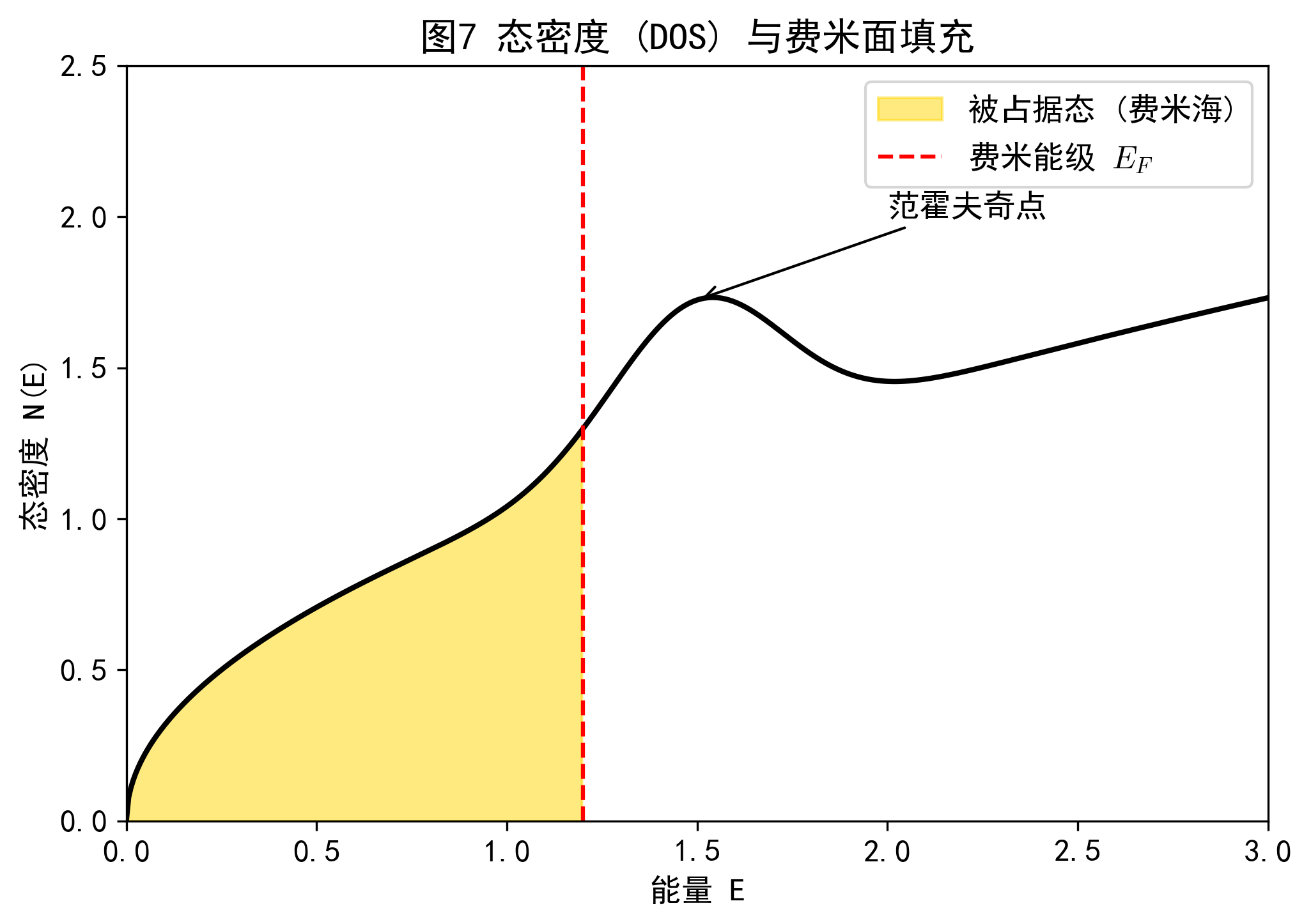
积分在等能面上进行。当群速度 $|\nabla_{\vec{k}} E| = 0$ 时（如能带极值点），$N(E)$ 出现范霍夫奇点。这是连接能带结构与实验谱学（如X射线发射谱）的关键纽带。

费米面

在绝对零度下，电子填充的最高能级对应的等能面称为费米面 $E(\vec{k}_F) = E_F$。费米面将 $k$ 空间分为占据区和非占据区。

• 金属：费米面穿过能带，存在半满带，导电性好。
• 绝缘体/半导体：费米面位于能隙之中（满带），导电性差。

经典的 $\sqrt{E}$ 态密度曲线叠加范霍夫奇点，金色区域填充表示费米海，红色虚线为费米能级。

八、非理想情形——赝势与表面态

赝势方法

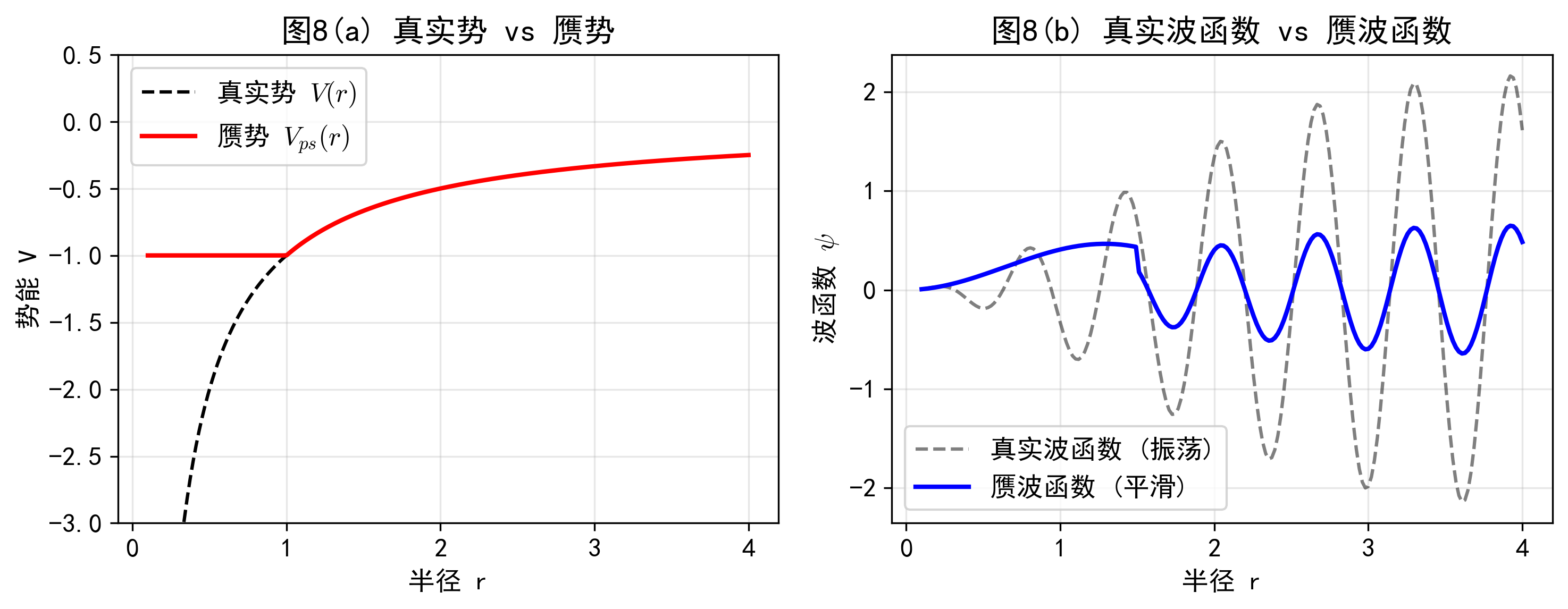
为了解释为何强势场的金属（如Al）也能用近自由电子近似描述，引入赝势。价电子波函数为了与芯电子正交，在核附近剧烈振荡，产生的动能抵消了核的强吸引势。剩余的有效势（赝势）很弱，使得微扰论重新适用。

表面电子态

晶体表面的存在破坏了周期性。在表面处，薛定谔方程允许存在复数波矢 $k = i\mu$ 的解。这种波函数在晶体内部指数衰减，在真空中也衰减，电子被局域在表面附近，形成位于能隙中的表面态（Tamm态/Shockley态）。

对比了原子核附近的深势阱（虚线）与平滑的赝势（实线），以及对应的急剧振荡波函数与平滑赝波函数。

重要核心理论的回顾与推导

能带理论的核心在于周期性。因为晶格的周期性，哈密顿量有了特殊的对称性，从而决定了波函数的布洛赫形式。接着，为了算出具体的$E(\vec{k})$关系，我们必须针对势场的强弱，采取不同的微扰策略。最后，通过统计物理（费米面和能态密度）将微观能级与宏观性质联系起来。

下面将以最严谨的逻辑链条和标准的数学语言，重构这四大核心板块。

一、布洛赫定理的推导与物理本质

物理逻辑起点

晶体中单电子薛定谔方程为：
$$ \hat{H} \psi(\vec{r}) = \left[ -\frac{\hbar^2}{2m}\nabla^2 + V(\vec{r}) \right] \psi(\vec{r}) = E \psi(\vec{r}) $$
其中势场满足晶格周期性：
$$ V(\vec{r} + \vec{R}_n) = V(\vec{r}) $$
这一周期性暗示了平移对称性。为了利用这一对称性，我们引入平移算符 $\hat{T}_{\vec{R}_n}$。

算符对易性证明

定义平移算符的作用是将函数坐标平移 $\vec{R}_n$：
$$ \hat{T}_{\vec{R}_n} f(\vec{r}) = f(\vec{r} + \vec{R}_n) $$
考察哈密顿量在平移操作下的性质：
$$ \hat{T}_{\vec{R}_n} \hat{H}(\vec{r}) \psi(\vec{r}) = \hat{H}(\vec{r} + \vec{R}_n) \psi(\vec{r} + \vec{R}_n) $$
由于势场和动能算符（拉普拉斯算符）都具有平移不变性，即 $\hat{H}(\vec{r} + \vec{R}_n) = \hat{H}(\vec{r})$，因此：
$$ \hat{T}_{\vec{R}_n} \hat{H} = \hat{H} \hat{T}_{\vec{R}_n} $$
即平移算符与哈密顿量对易：
$$ [\hat{H}, \hat{T}_{\vec{R}_n}] = 0 $$
根据量子力学原理，对易算符具有共同的本征函数。

本征值的确定

设 $\psi(\vec{r})$ 同时是 $\hat{H}$ 和 $\hat{T}_{\vec{R}_n}$ 的本征函数，对应的平移本征值为 $\lambda_{\vec{R}_n}$：
$$ \hat{T}_{\vec{R}_n} \psi(\vec{r}) = \psi(\vec{r} + \vec{R}_n) = \lambda_{\vec{R}_n} \psi(\vec{r}) $$
由于波函数必须归一化（或在无限晶体中保持有界），本征值的模必须为 1：
$$ |\lambda_{\vec{R}_n}| = 1 $$
这就意味着 $\lambda_{\vec{R}_n}$ 必须是一个纯相位因子。考虑到平移的加法性质 $\hat{T}_{\vec{R}_n} \hat{T}_{\vec{R}_m} = \hat{T}_{\vec{R}_n + \vec{R}_m}$，本征值必须满足指数形式：
$$ \lambda_{\vec{R}_n} = e^{i \vec{k} \cdot \vec{R}_n} $$
这里的 $\vec{k}$ 就是引入的量子数——简约波矢。

布洛赫函数形式

综上，波函数满足性质：
$$ \psi_{\vec{k}}(\vec{r} + \vec{R}_n) = e^{i \vec{k} \cdot \vec{R}_n} \psi_{\vec{k}}(\vec{r}) $$
为了满足此式，我们可以构造解的形式：
$$ \psi_{\vec{k}}(\vec{r}) = e^{i \vec{k} \cdot \vec{r}} u_{\vec{k}}(\vec{r}) $$
代入上式验证 $u_{\vec{k}}(\vec{r})$ 的性质：
$$ e^{i \vec{k} \cdot (\vec{r} + \vec{R}_n)} u_{\vec{k}}(\vec{r} + \vec{R}_n) = e^{i \vec{k} \cdot \vec{R}_n} e^{i \vec{k} \cdot \vec{r}} u_{\vec{k}}(\vec{r}) $$
消去相同项得到：
$$ u_{\vec{k}}(\vec{r} + \vec{R}_n) = u_{\vec{k}}(\vec{r}) $$
结论： 晶体电子波函数是由平面波 $e^{i \vec{k} \cdot \vec{r}}$ 和一个具有晶格周期性的函数 $u_{\vec{k}}(\vec{r})$ 调制而成的。

二、近自由电子近似（弱势场微扰）

物理逻辑

势场 $V(\vec{r})$ 很弱，可以作为微扰处理。零级近似是自由电子平面波。问题的核心在于处理布里渊区边界附近的简并微扰。

能量修正公式

势场展开为傅里叶级数：
$$ V(\vec{r}) = \sum_{\vec{G}} V_{\vec{G}} e^{i \vec{G} \cdot \vec{r}} $$
根据微扰论，二级能量修正为：
$$ E_{\vec{k}} = E_{\vec{k}}^0 + V_0 + \sum_{\vec{G} \neq 0} \frac{|V_{\vec{G}}|^2}{E_{\vec{k}}^0 - E_{\vec{k}-\vec{G}}^0} $$
其中零级能量 $E_{\vec{k}}^0 = \frac{\hbar^2 k^2}{2m}$。

简并微扰与久期方程

当波矢 $\vec{k}$ 接近布里渊区边界时，满足布拉格反射条件：
$$ (\vec{k} - \vec{G})^2 \approx k^2 \implies E_{\vec{k}-\vec{G}}^0 \approx E_{\vec{k}}^0 $$
此时分母趋于零，微扰论失效，必须使用简并微扰论。取 $\psi$ 为两个简并态 $|\vec{k}\rangle$ 和 $|\vec{k}-\vec{G}\rangle$ 的线性组合：
$$ \psi = c_1 e^{i \vec{k} \cdot \vec{r}} + c_2 e^{i (\vec{k} - \vec{G}) \cdot \vec{r}} $$
代入薛定谔方程，利用正交性，得到系数 $c_1, c_2$ 的线性方程组，其有非零解的条件是系数行列式（久期方程）为零：
$$ \begin{vmatrix} E_{\vec{k}}^0 - E & V_{\vec{G}} \\ V_{\vec{G}}^* & E_{\vec{k}-\vec{G}}^0 - E \end{vmatrix} = 0 $$

能隙的产生

在布里渊区边界上，严格满足 $E_{\vec{k}}^0 = E_{\vec{k}-\vec{G}}^0$。解上述二次方程：
$$ (E_{\vec{k}}^0 - E)^2 - |V_{\vec{G}}|^2 = 0 $$
得到两个解：
$$ E_{\pm} = E_{\vec{k}}^0 \pm |V_{\vec{G}}| $$
由此产生的能量差（禁带宽度）为：
$$ E_g = E_+ - E_- = 2|V_{\vec{G}}| $$
结论： 能带在布里渊区边界断开，禁带宽度取决于晶体势场在该处的傅里叶分量模的两倍。

三、紧束缚近似（原子轨道线性组合 LCAO）

物理逻辑

势场很强，电子主要被束缚在原子核周围。晶体波函数由孤立原子的本征态 $\phi(\vec{r})$ 线性叠加而成。

试探波函数

构造满足布洛赫定理的线性组合（布洛赫和）：
$$ \psi_{\vec{k}}(\vec{r}) = \frac{1}{\sqrt{N}} \sum_{\vec{R}_n} e^{i \vec{k} \cdot \vec{R}_n} \phi(\vec{r} - \vec{R}_n) $$
其中 $\phi(\vec{r})$ 是满足 $\hat{H}_{at} \phi = E_0 \phi$ 的原子轨道。

能量期望值计算

晶体哈密顿量为 $\hat{H} = \hat{H}_{at} + \Delta U(\vec{r})$，其中 $\Delta U$ 是其他原子的微扰势。计算能量期望值：
$$ E(\vec{k}) = \langle \psi_{\vec{k}} | \hat{H} | \psi_{\vec{k}} \rangle $$
展开积分（假设不同格点原子轨道正交归一）：
$$ E(\vec{k}) \approx \sum_{\vec{R}_n} e^{i \vec{k} \cdot \vec{R}_n} \int \phi^*(\vec{r}) \hat{H} \phi(\vec{r} - \vec{R}_n) d\tau $$
将积分分为两部分讨论：

1. 本位项 ($\vec{R}_n = 0$)：
   $$ E_0 - \int \phi^*(\vec{r}) [-\Delta U(\vec{r})] \phi(\vec{r}) d\tau = E_0 - C $$
   这里 $C$ 是库仑积分（位移能），表示原子能级的整体平移。
2. 近邻项 ($\vec{R}_n = \vec{\delta}$)：
   $$ -\int \phi^*(\vec{r}) [-\Delta U(\vec{r})] \phi(\vec{r} - \vec{\delta}) d\tau = -J(\vec{\delta}) $$
   这里 $J$ 是交叠积分（或跳跃积分，Transfer Integral），决定了能带的宽度。

色散关系推导

只考虑最近邻原子相互作用，求和公式简化为：
$$ E(\vec{k}) = E_0 - C - \sum_{\vec{\delta}} J(\vec{\delta}) e^{i \vec{k} \cdot \vec{\delta}} $$
以简单立方晶格（晶格常数 $a$）为例，最近邻矢量为 $(\pm a, 0, 0)$ 等6个。假设 $s$ 态各向同性，即 $J$ 相等：
$$ \sum_{\vec{\delta}} e^{i \vec{k} \cdot \vec{\delta}} = e^{ik_x a} + e^{-ik_x a} + \cdots = 2(\cos k_x a + \cos k_y a + \cos k_z a) $$
最终能带公式：
$$ E(\vec{k}) = E_0 - C - 2J (\cos k_x a + \cos k_y a + \cos k_z a) $$
结论： 原子能级展宽成能带，带宽与交叠积分 $J$ 成正比。

四、能态密度与费米面

能态密度 $N(E)$

定义：单位能量间隔、单位体积内的量子态数目。
$$ N(E) dE = \frac{1}{V} \times (\text{k空间体积元内状态数}) \times 2 (\text{自旋}) $$
由于 $k$ 空间状态密度均匀为 $V/(2\pi)^3$，则：
$$ N(E) dE = \frac{2}{(2\pi)^3} \int_{E}^{E+dE} d^3k $$
将积分变换为对等能面 $S_E$ 的面积分，利用 $dE = |\nabla_{\vec{k}} E| dk_{\perp}$：
$$ d^3k = dS \cdot dk_{\perp} = dS \frac{dE}{|\nabla_{\vec{k}} E|} $$
代入得到能态密度通用公式：
$$ N(E) = \frac{1}{4\pi^3} \int_{S_E} \frac{dS}{|\nabla_{\vec{k}} E|} $$
关键点： 当群速度 $v_g = \frac{1}{\hbar}\nabla_{\vec{k}} E = 0$ 时（如能带顶或底），$N(E)$ 会出现奇异点（范霍夫奇点）。

费米面

定义：在绝对零度下，电子填充的最高能级对应的等能面。
$$ E_F = E(\vec{k}_F) $$
对于自由电子气，能量各向同性：
$$ E = \frac{\hbar^2 k^2}{2m} $$
费米面是一个球面。根据费米波矢 $k_F$ 与电子浓度 $n$ 的关系：
$$ k_F = (3\pi^2 n)^{1/3} $$
费米能量：
$$ E_F = \frac{\hbar^2}{2m} (3\pi^2 n)^{2/3} $$
物理意义：

• 费米面将 $k$ 空间分为已占据态（内部）和未占据态（外部）。
• 金属的导电性取决于费米面附近的电子在电场下的微小跃迁。
• 如果费米面填满了整个布里渊区（满带），且与下一能带有能隙，则为绝缘体或半导体。