理论推导与归纳
晶格热容的经典理论
经典物理学认为,对于 $N$ 个原子组成的晶体,共有 $3N$ 个简谐振动模。根据能量均分定理,每个振动模的平均能量是 $k_B T$,总平均能量 $\bar{E}$ 和摩尔热容 $C_V$ 为:
$$\bar{E} = 3 N k_B T$$
$$C_V = \left(\frac{\partial \bar{E}}{\partial T}\right)_V = 3 N k_B$$
摩尔固体热容为:
$$C_V = 3 N_A k_B = 3 R$$
这被称为杜隆-珀替定律(Dulong-Petit Law)。该定律与高温实验结果相符,但在低温下(实验表明 $T \to 0$ 时 $C_V \to 0$)与实验结果严重不符。
量子理论下的单个振动模平均能量
根据量子理论,频率为 $\omega_j$ 的简谐振动模的能量是量子化的,能级为 $E_{n_j} = \left(n_j + \frac{1}{2}\right) \hbar \omega_j$。利用玻尔兹曼统计,该振动模在温度 $T$ 时的平均能量 $\bar{E}_j(T)$ 为:
$$\bar{E}_j(T) = \sum_{n_j} P_{n_j} E_{n_j} = \frac{\hbar \omega_j}{2} + \frac{\hbar \omega_j}{e^{\hbar \omega_j/k_B T} - 1}$$
其中第一项 $\frac{1}{2}\hbar \omega_j$ 是零点能(Zero-Point Energy),与温度无关;第二项是平均热能(Average Thermal Energy)。
单个振动模对热容的贡献
对平均能量 $\bar{E}_j(T)$ 关于温度 $T$ 求导,即可得到该振动模对定容热容 $C_{V_j}$ 的贡献:
$$C_{V_j} = \left(\frac{d \bar{E}_j}{d T}\right)_V$$
$$C_{V_j} = k_B \left(\frac{\hbar \omega_j}{k_B T}\right)^2 \frac{e^{\hbar \omega_j/k_B T}}{(e^{\hbar \omega_j/k_B T} - 1)^2}$$
晶体总热容是所有 $3N$ 个振动模贡献的总和:
$$C_V = \sum_{j=1}^{3N} C_{V_j}$$
爱因斯坦模型推导与分析
爱因斯坦模型假设
爱因斯坦模型(Einstein Model, 1907)假设晶体中所有 $3N$ 个振动模都具有相同的频率 $\omega_0$。
总平均能量和热容公式
将 $\omega_j = \omega_0$ 代入单个振动模的平均能量公式,总平均能量 $\bar{E}$ 为 $3N$ 倍的单个模平均能量:
$$\bar{E} = \sum_{j=1}^{3N} \bar{E}_j(T) = 3N \left(\frac{1}{2}\hbar \omega_0 + \frac{\hbar \omega_0}{e^{\hbar \omega_0/k_B T} - 1}\right)$$
晶体的定容热容 $C_V$ 为:
$$C_V = \left(\frac{\partial \bar{E}}{\partial T}\right)_V$$
$$C_V = 3 N k_B \left(\frac{\hbar \omega_0}{k_B T}\right)^2 \frac{e^{\hbar \omega_0/k_B T}}{(e^{\hbar \omega_0/k_B T} - 1)^2}$$
引入爱因斯坦温度 $\Theta_E$:
$$\hbar \omega_0 = k_B \Theta_E \quad \Rightarrow \quad \frac{\hbar \omega_0}{k_B T} = \frac{\Theta_E}{T}$$
热容公式可写为:
$$C_V = 3 N k_B \left(\frac{\Theta_E}{T}\right)^2 \frac{e^{\Theta_E/T}}{(e^{\Theta_E/T} - 1)^2}$$
高温极限 ($T \gg \Theta_E$)
当 $T$ 很高时,$\frac{\hbar \omega_0}{k_B T} = x \ll 1$。利用泰勒展开 $e^x \approx 1 + x + \frac{1}{2} x^2 + \dots$:
$$e^{\Theta_E/T} \approx 1 + \frac{\Theta_E}{T}$$
$$(e^{\Theta_E/T} - 1)^2 \approx \left(\frac{\Theta_E}{T}\right)^2$$
$$C_V \approx 3 N k_B \left(\frac{\Theta_E}{T}\right)^2 \frac{1 + \Theta_E/T}{\left(\Theta_E/T\right)^2} \approx 3 N k_B$$
结果符合杜隆-珀替定律。
低温极限 ($T \ll \Theta_E$)
当 $T$ 很低时,$\frac{\hbar \omega_0}{k_B T} = x \gg 1$。此时 $e^{\Theta_E/T} \gg 1$:
$$C_V \approx 3 N k_B \left(\frac{\Theta_E}{T}\right)^2 \frac{e^{\Theta_E/T}}{\left(e^{\Theta_E/T}\right)^2} = 3 N k_B \left(\frac{\Theta_E}{T}\right)^2 e^{-\Theta_E/T}$$
$C_V$ 按温度的指数形式迅速趋于零。
爱因斯坦模型总结
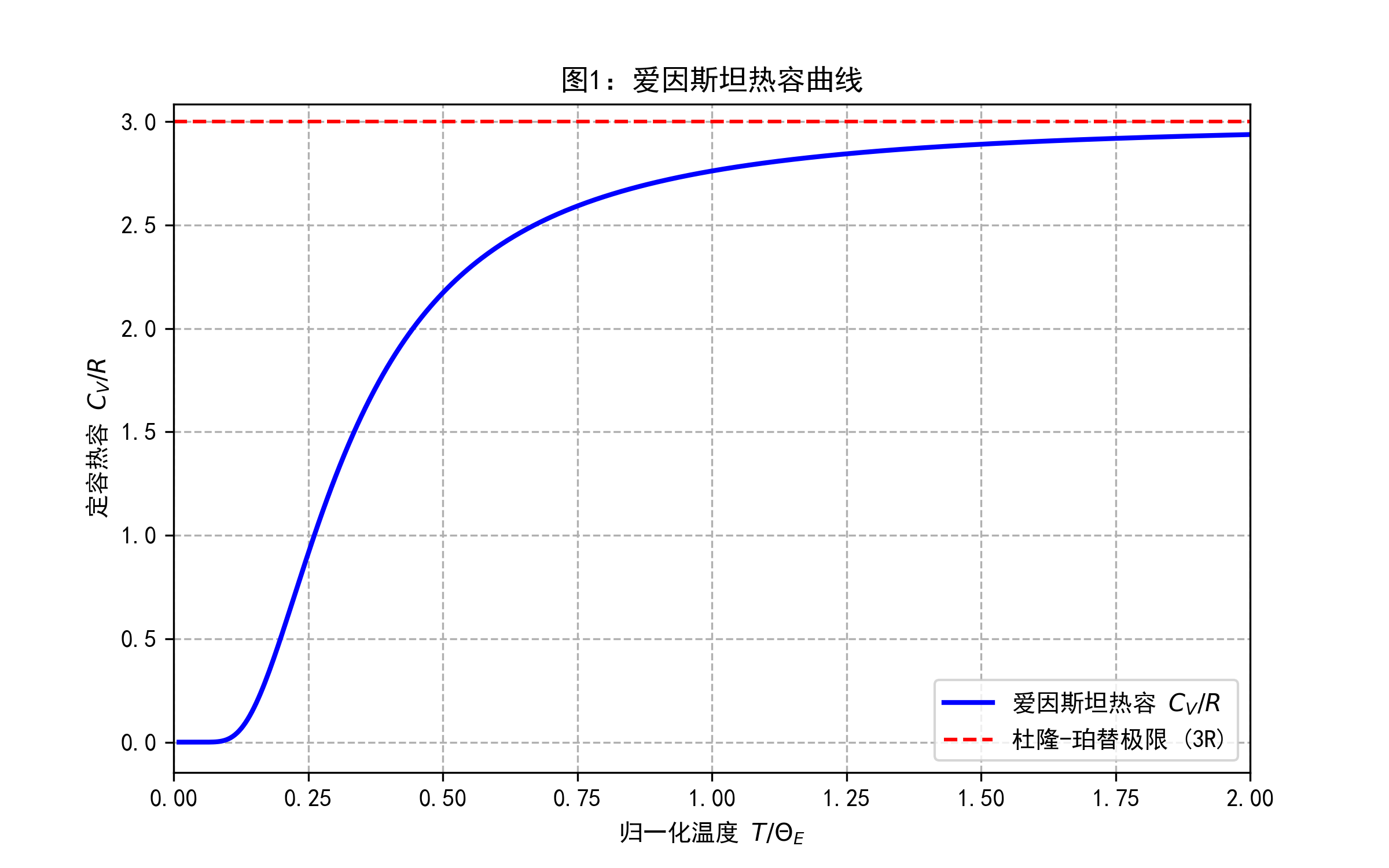
该图展示了爱因斯坦模型预测的定容热容 $C_V$ 随温度 $T$ 的变化趋势,以 $C_V/R$ 对 $T/\Theta_E$ 归一化。
爱因斯坦模型成功地解释了热容随温度降低而迅速趋于零的趋势,克服了经典理论的困难。然而,它预测的低温行为是指数下降,与实验测得的 $C_V \propto T^3$ 规律不符。缺陷在于它忽略了格波的色散关系,认为所有振动模频率相同。
晶格振动模式密度
为了计算总热容 $C_V = \sum C_{V_j}$,需要知道不同频率 $\omega$ 的振动模的数目。晶格振动模式密度 $g(\omega)$ 就是解决这个问题引入的,它表示单位频率间隔内的振动模式数目。
模式密度定义
$$g(\omega) = \lim_{\Delta \omega \to 0} \frac{\Delta n}{\Delta \omega}$$
$\vec{q}$ 空间状态密度
在 $\vec{q}$ 空间(波矢空间)中,晶格振动模均匀分布,状态密度为 $\frac{V}{(2\pi)^3}$($V$ 是晶体体积)。在 $\vec{q}$ 空间中,$\omega \to \omega + d\omega$ 之间的振动模数目 $d n$ 为:
$$d n = \frac{V}{(2\pi)^3} \int_{\omega=\text{const}}^{\omega+d\omega} d \vec{q}$$
模式密度的一般表达式(三维)
在 $\vec{q}$ 空间中,两个等频率面 $\omega$ 和 $\omega + d\omega$ 之间的体积元 $d \vec{q}$ 可写成 $d s \cdot d q$,其中 $d s$ 是等频率面 $\omega(\vec{q}) = \text{const}$ 的面积元, $d q$ 是垂直于等频率面的厚度。利用 $d \omega = |\nabla_q \omega(\vec{q})| d q$,得到 $d q = \frac{d \omega}{|\nabla_q \omega(\vec{q})|}$。
$$d n = \frac{V}{(2\pi)^3} \int_{\omega=\text{const}} d s \cdot d q = \frac{V}{(2\pi)^3} \int_{\omega=\text{const}} \frac{d s}{|\nabla_q \omega(\vec{q})|} d \omega$$
所以模式密度 $g(\omega)$ 为:
$$g(\omega) = \frac{d n}{d \omega} = \frac{V}{(2\pi)^3} \int_{\omega(\vec{q})=\omega} \frac{d s}{|\nabla_q \omega(\vec{q})|}$$
德拜模型推导与分析
德拜模型假设:线性色散关系
德拜模型(Debye Model, 1912)将晶体视为连续介质,假设振动频率与波矢成正比(线性色散关系):
$$\omega = c q$$
其中 $c$ 为声速(纵波 $c_L$,横波 $c_T$)。
模式密度 $g(\omega)$ 的推导
对于 $\omega = c q$,等频率面是一个半径为 $q$ 的球面,其面积 $s = 4 \pi q^2$。梯度 $|\nabla_q \omega(\vec{q})| = c$。
代入模式密度一般表达式:
$$g(\omega) = \sum_s \frac{V}{(2\pi)^3} \frac{4\pi q^2}{c_s}$$
其中 $s$ 代表三个声学支(一个纵波 $c_L$ 和两个横波 $c_T$):
$$g(\omega) = \frac{V}{2\pi^2} \left(\frac{1}{c_L^3} + \frac{2}{c_T^3}\right) \omega^2$$
引入平均声速 $\bar{C}$:
$$\frac{3}{\bar{C}^3} = \frac{1}{c_L^3} + \frac{2}{c_T^3}$$
德拜模型下的模式密度为:
$$g(\omega) = \frac{3V}{2\pi^2 \bar{C}^3} \omega^2$$
德拜模式密度具有 $\omega^2$ 依赖性。
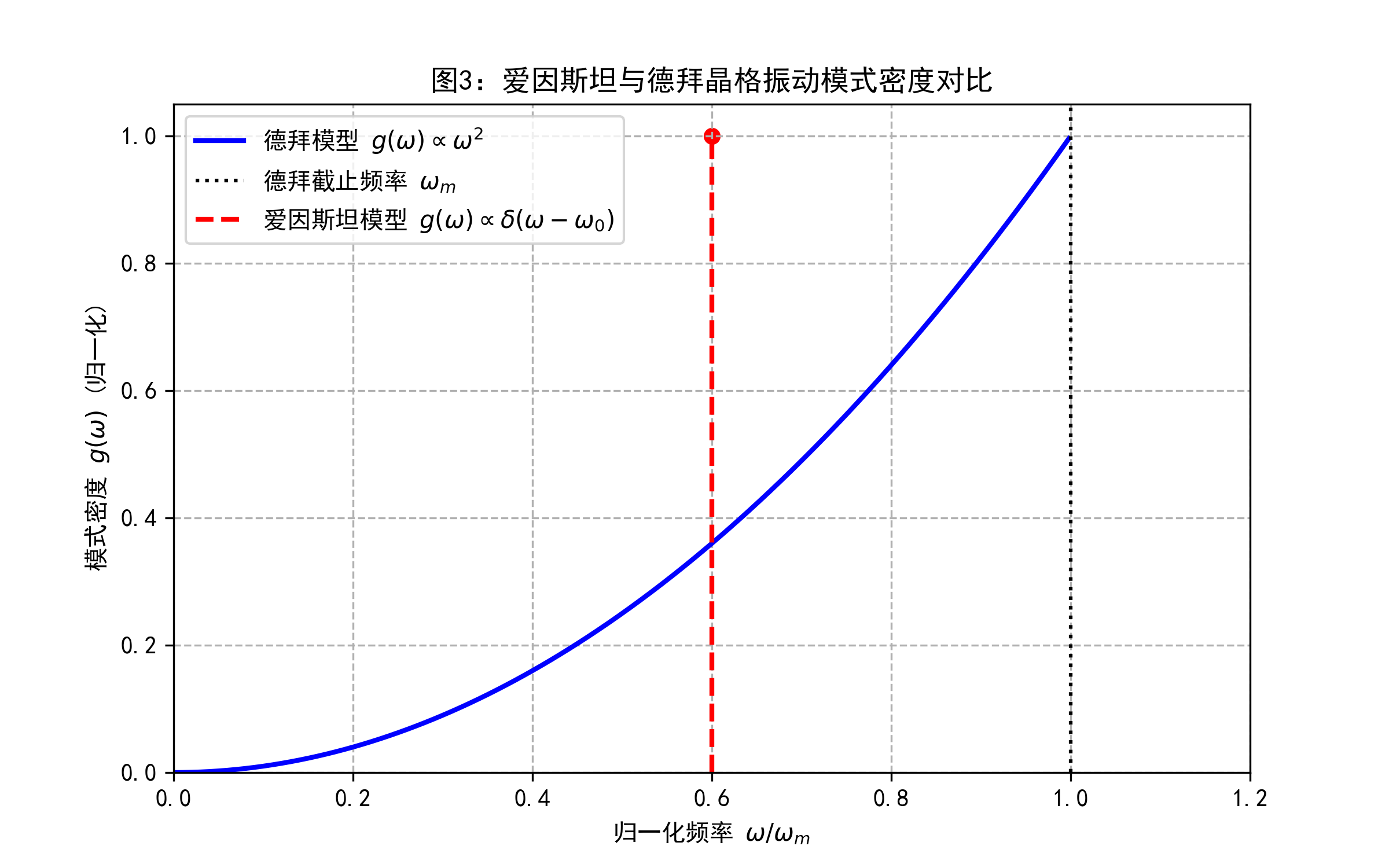
该图对比了爱因斯坦模型和德拜模型对晶格振动模式密度 $g(\omega)$ 的假设。爱因斯坦:所有模式集中在 $\omega_0$ (用$\delta$函数表示)。德拜:$g(\omega) \propto \omega^2$ (抛物线),直到截止频率 $\omega_m$。
德拜截止频率 $\omega_m$
德拜模型引入一个最大截止频率 $\omega_m$,要求总格波的数目等于 $3N$:
$$\int_0^{\omega_m} g(\omega) d\omega = 3 N$$
$$\int_0^{\omega_m} \frac{3V}{2\pi^2 \bar{C}^3} \omega^2 d\omega = 3 N$$
$$\frac{3V}{2\pi^2 \bar{C}^3} \frac{\omega_m^3}{3} = 3 N$$
$$\omega_m^3 = 6 \pi^2 \bar{C}^3 \frac{N}{V} \quad \Rightarrow \quad \omega_m = \bar{C} \left(6 \pi^2 \frac{N}{V}\right)^{1/3}$$
引入德拜温度 $\Theta_D$:
$$\hbar \omega_m = k_B \Theta_D$$
晶体总热容(德拜热容)
将 $g(\omega)$ 和 $C_{V_j}$(用 $\omega$ 代替 $\omega_j$)代入总热容的积分形式:
$$C_V = \int_0^{\omega_m} k_B \left(\frac{\hbar \omega}{k_B T}\right)^2 \frac{e^{\hbar \omega/k_B T}}{(e^{\hbar \omega/k_B T} - 1)^2} g(\omega) d\omega$$
代入 $g(\omega)$ 的表达式:
$$C_V = \int_0^{\omega_m} k_B \left(\frac{\hbar \omega}{k_B T}\right)^2 \frac{e^{\hbar \omega/k_B T}}{(e^{\hbar \omega/k_B T} - 1)^2} \frac{3V}{2\pi^2 \bar{C}^3} \omega^2 d\omega$$
进行变量替换 $\xi = \frac{\hbar \omega}{k_B T}$,则 $\omega = \frac{k_B T}{\hbar} \xi$, $d\omega = \frac{k_B T}{\hbar} d\xi$。积分上限变为 $\xi_m = \frac{\hbar \omega_m}{k_B T} = \frac{\Theta_D}{T}$。
$$C_V = 9 N k_B \left(\frac{T}{\Theta_D}\right)^3 \int_0^{\Theta_D/T} \frac{\xi^4 e^\xi}{(e^\xi - 1)^2} d\xi$$
这被称为德拜热容函数的表达式。
高温极限 ($T \gg \Theta_D$)
当 $T$ 很高时,$\frac{\Theta_D}{T} \ll 1$,积分上限很小。利用 $e^\xi \approx 1 + \xi$ 和 $(e^\xi - 1)^2 \approx \xi^2$ 的近似:
$$C_V \approx 9 N k_B \left(\frac{T}{\Theta_D}\right)^3 \int_0^{\Theta_D/T} \frac{\xi^4 (1+\xi)}{\xi^2} d\xi$$
$$C_V \approx 9 N k_B \left(\frac{T}{\Theta_D}\right)^3 \int_0^{\Theta_D/T} \xi^2 d\xi = 9 N k_B \left(\frac{T}{\Theta_D}\right)^3 \frac{1}{3} \left(\frac{\Theta_D}{T}\right)^3 = 3 N k_B$$
结果符合杜隆-珀替定律。
低温极限 ($T \ll \Theta_D$)
当 $T$ 很低时,$\frac{\Theta_D}{T} \to \infty$,积分上限趋于无穷。积分 $\int_0^\infty \frac{\xi^4 e^\xi}{(e^\xi - 1)^2} d\xi = \frac{4\pi^4}{15}$。
$$C_V \approx 9 N k_B \left(\frac{T}{\Theta_D}\right)^3 \frac{4\pi^4}{15}$$
$$C_V = \frac{12\pi^4}{5} N k_B \left(\frac{T}{\Theta_D}\right)^3$$
$$C_V \propto T^3$$
结果符合实验的德拜 $T^3$ 定律(Debye $T^3$ Law)。
德拜模型总结
该图展示了德拜模型预测的定容热容 $C_V$ 随温度 $T$ 的变化趋势,并与低温时的 $T^3$ 定律进行了对比。
德拜模型通过引入格波的色散关系(线性 $\omega = c q$)和最大截止频率 $\omega_m$,成功解释了晶体在高温下遵循杜隆-珀替定律,在极低温下热容正比于 $T^3$ 的实验规律,是比爱因斯坦模型更精确的量子理论。
德拜与爱因斯坦模型的对比
| 特点 | 爱因斯坦模型 (Einstein Model) | 德拜模型 (Debye Model) |
|---|---|---|
| 基本假设 | 所有 $3N$ 个振动模频率相同 ($\omega_0$)。 | 晶体是连续介质,格波色散关系线性 ($\omega = c q$),有截止频率 ($\omega_m$)。 |
| 模式密度 $g(\omega)$ | $g(\omega) \propto \delta(\omega - \omega_0)$ (离散频率) | $g(\omega) \propto \omega^2$ (连续频率) |
| 低温热容 ($T \ll \Theta$) | $C_V \propto e^{-\Theta_E/T}$ (指数下降) | $C_V \propto T^3$ (德拜 $T^3$ 定律) |
| 高温热容 ($T \gg \Theta$) | $C_V \approx 3R$ (杜隆-珀替定律) | $C_V \approx 3R$ (杜隆-珀替定律) |
| 准确性 | 仅定性正确($C_V \to 0$),低温定量不符。 | 低温定量准确,高温准确。 |
德拜模型在低温下准确的原因在于,在极低温时,只有长波(小波矢 $q$)的声子被激发,而这些长波声子的色散关系 ($\omega \propto q$) 正是德拜模型的基础假设。爱因斯坦模型由于忽略了频率分布的细节,在低温下失效。
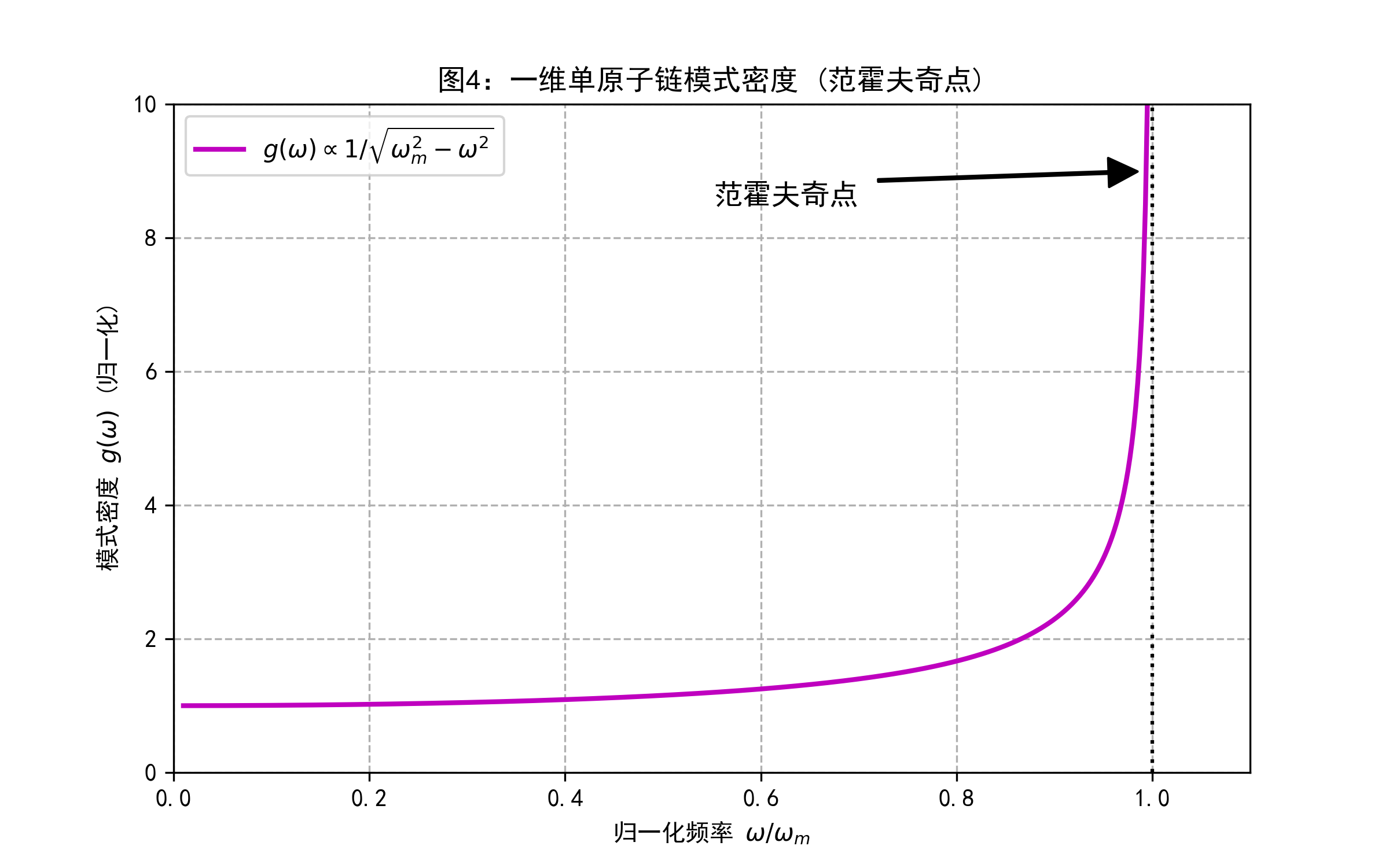
该图展示了一维单原子链的晶格振动模式密度 $g(\omega)$。其表达式为 $g(\omega) \propto \frac{1}{\sqrt{\omega_m^2 - \omega^2}}$。在 $\omega \to \omega_m$ 处,$g(\omega)$ 趋于无穷,这被称为范霍夫奇点(Van Hove Singularity)。
补充:德拜模型中的声学支与模式密度
晶体中的弹性波
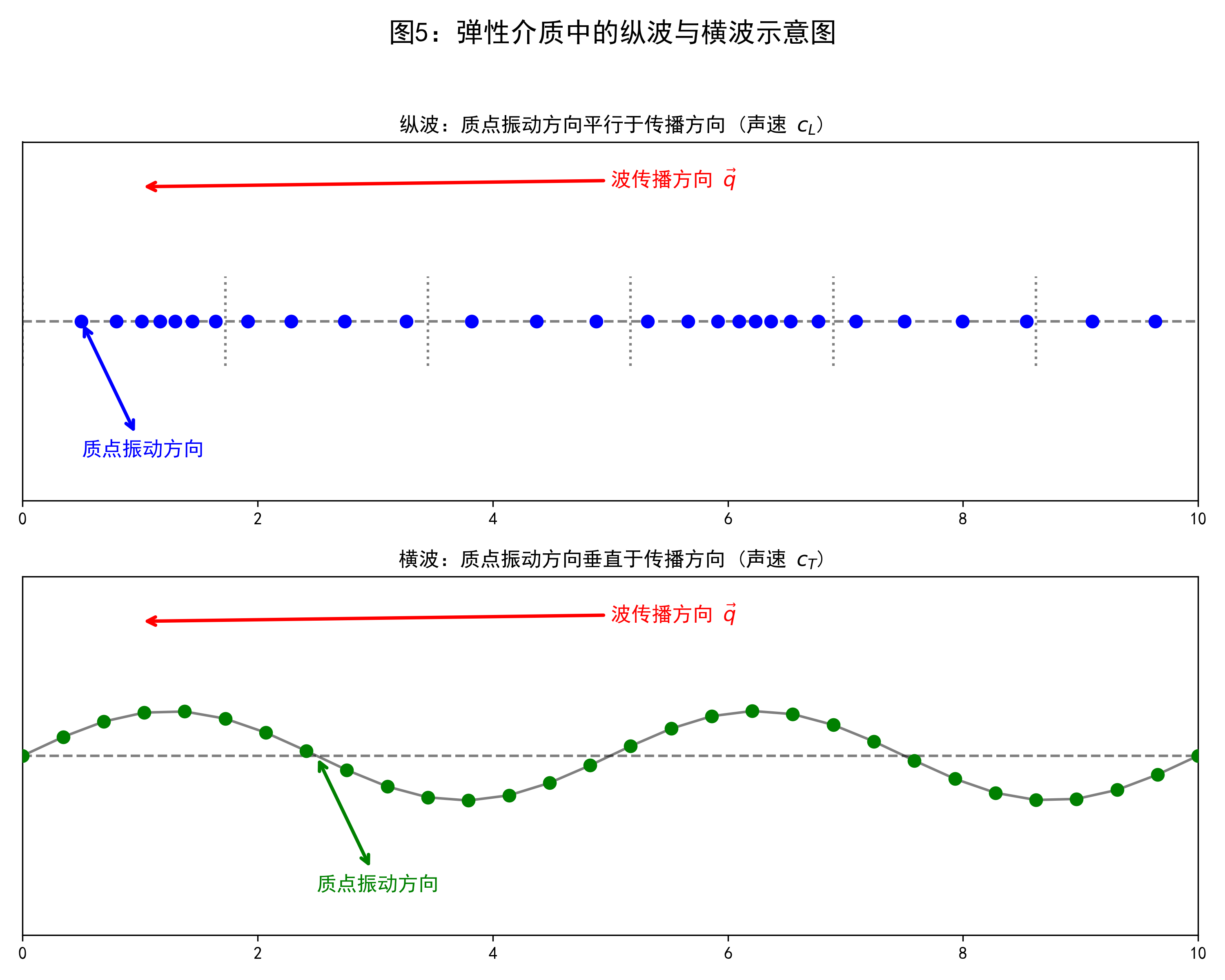
在德拜模型中,晶体被近似视为各向同性的连续弹性介质。在这种介质中传播的格波可以看作是弹性波,它们可以分为两种基本类型:
- 纵波 (Longitudinal Wave): 质点的振动方向平行于波的传播方向(波矢 $\vec{q}$ 的方向)。
- 横波 (Transverse Wave): 质点的振动方向垂直于波的传播方向(波矢 $\vec{q}$ 的方向)。
纵波(上图):展示质点(蓝点)沿 $x$ 轴(波的传播方向)振动,造成疏密变化。
横波(下图):展示质点(绿点)沿 $y$ 轴(垂直于波的传播方向)振动,形成起伏的波形。
红色箭头表示波的传播方向 $\vec{q}$,蓝色和绿色箭头表示质点的振动方向,以清晰对比两种波的特征。
对于一个三维介质,沿着任意一个波矢 $\vec{q}$ 的方向,总共有三个独立的振动模式:
- 一个纵波分支 (Lognitudinal Wave):对应一个纵波声速 $c_L$。
- 两个独立的横波分支 (Transverse Wave):对应两个方向互相垂直的横波,具有相同的横波声速 $c_T$(由于介质是各向同性的)。
因此,总共有 $s=3$ 个声学分支。
线性色散关系
对于弹性波(在 $\vec{q}$ 较小时,即长波近似下),频率 $\omega$ 与波矢 $q$ 成正比(线性色散关系):
$$\omega = c_s q$$
其中 $s$ 是声波的分支,取值 $L, T_1, T_2$。 $c_s$ 是对应的声速。
模式密度中的声学支贡献
晶体总的振动模式密度 $g(\omega)$ 是所有分支(三个声学支)模式密度贡献的总和:
$$g(\omega) = \sum_{s=L, T_1, T_2} g_s(\omega)$$
对于任意一个分支 $s$,其模式密度的通用公式为(三维):
$$g_s(\omega) = \frac{V}{(2\pi)^3} \int_{\omega_s(\vec{q})=\omega} \frac{d s}{|\nabla_q \omega_s(\vec{q})|}$$
对于线性色散关系 $\omega = c_s q$,我们有:
- 等频率面是一个半径为 $q = \omega/c_s$ 的球面,其面积 $d s = 4\pi q^2 = 4\pi \left(\frac{\omega}{c_s}\right)^2$。
- 梯度 $|\nabla_q \omega_s(\vec{q})| = c_s$。
代入公式,单个声学分支 $s$ 的模式密度为:
$$g_s(\omega) = \frac{V}{(2\pi)^3} \frac{4\pi (\omega/c_s)^2}{c_s}$$
$$g_s(\omega) = \frac{V}{2\pi^2 c_s^3} \omega^2$$
晶体总模式密度推导
晶体总模式密度 $g(\omega)$ 是三个声学分支的模式密度之和:
$$g(\omega) = g_L(\omega) + g_{T_1}(\omega) + g_{T_2}(\omega)$$
由于介质是各向同性的,两个横波分支的速度相等,即 $c_{T_1} = c_{T_2} = c_T$。
$$g(\omega) = \frac{V}{2\pi^2 c_L^3} \omega^2 + \frac{V}{2\pi^2 c_T^3} \omega^2 + \frac{V}{2\pi^2 c_T^3} \omega^2$$
$$g(\omega) = \frac{V}{2\pi^2} \left(\frac{1}{c_L^3} + \frac{2}{c_T^3}\right) \omega^2$$
引入平均声速 $\bar{C}$
为了简化表达式,引入一个平均声速 $\bar{C}$,其定义基于对 $\frac{1}{c_s^3}$ 项的平均:
$$\frac{3}{\bar{C}^3} \equiv \frac{1}{c_L^3} + \frac{2}{c_T^3}$$
将此定义代入总模式密度 $g(\omega)$ 的表达式:
$$g(\omega) = \frac{V}{2\pi^2} \left(\frac{3}{\bar{C}^3}\right) \omega^2$$
$$g(\omega) = \frac{3V}{2\pi^2 \bar{C}^3} \omega^2$$
这个最终表达式是德拜模型中使用的模式密度函数,它正比于 $\omega^2$。
德拜截止频率与总格波数目
根据德拜模型的假设,该模式密度只在 $0 \le \omega \le \omega_m$ 的频率范围内有效,且总振动模式数目必须等于 $3N$:
$$\int_0^{\omega_m} g(\omega) d\omega = 3 N$$
$$\int_0^{\omega_m} \frac{3V}{2\pi^2 \bar{C}^3} \omega^2 d\omega = 3 N$$
$$\frac{3V}{2\pi^2 \bar{C}^3} \left[\frac{1}{3} \omega^3\right]_0^{\omega_m} = 3 N$$
$$\frac{V}{2\pi^2 \bar{C}^3} \omega_m^3 = 3 N$$
$$\omega_m^3 = \frac{6 \pi^2 \bar{C}^3 N}{V}$$
从而确定了德拜截止频率 $\omega_m$,它与晶体的体积 $V$、原子数 $N$ 以及平均声速 $\bar{C}$ 相关。这三个声学分支的贡献通过平均声速 $\bar{C}$ 的形式体现在德拜模型的热容计算中。
便签纸
看起来这篇笔记只有一个便签

小德
美国Level3 2025 November 19th晶格热容的量子理论通过爱因斯坦模型和更精确的德拜模型(引入线性色散关系和 $\omega^2$ 模式密度)成功解释了晶体热容在低温下快速趋于零(德拜模型更准确地预测了 $T^3$ 规律),而晶格振动谱 $\omega(\vec{q})$ 则主要通过中子非弹性散射来实验测定。